Classification and Regression
import math
# probability of class "buy"
p_buy = 0.40
# probability of class "not buy"
p_not_buy = 0.60
# calculate entropy
entropy = -(p_buy * math.log2(p_buy) +
p_not_buy * math.log2(p_not_buy))
# print out the result
print(entropy)0.9709505944546686from scipy.stats import entropy
# probability of class "buy"
p_buy = 0.40
# probability of class "not buy"
p_not_buy = 0.60
probabilities = [p_buy, p_not_buy]
# calculate entropy
entropy = entropy(probabilities, base=2)
print(entropy)0.9709505944546688
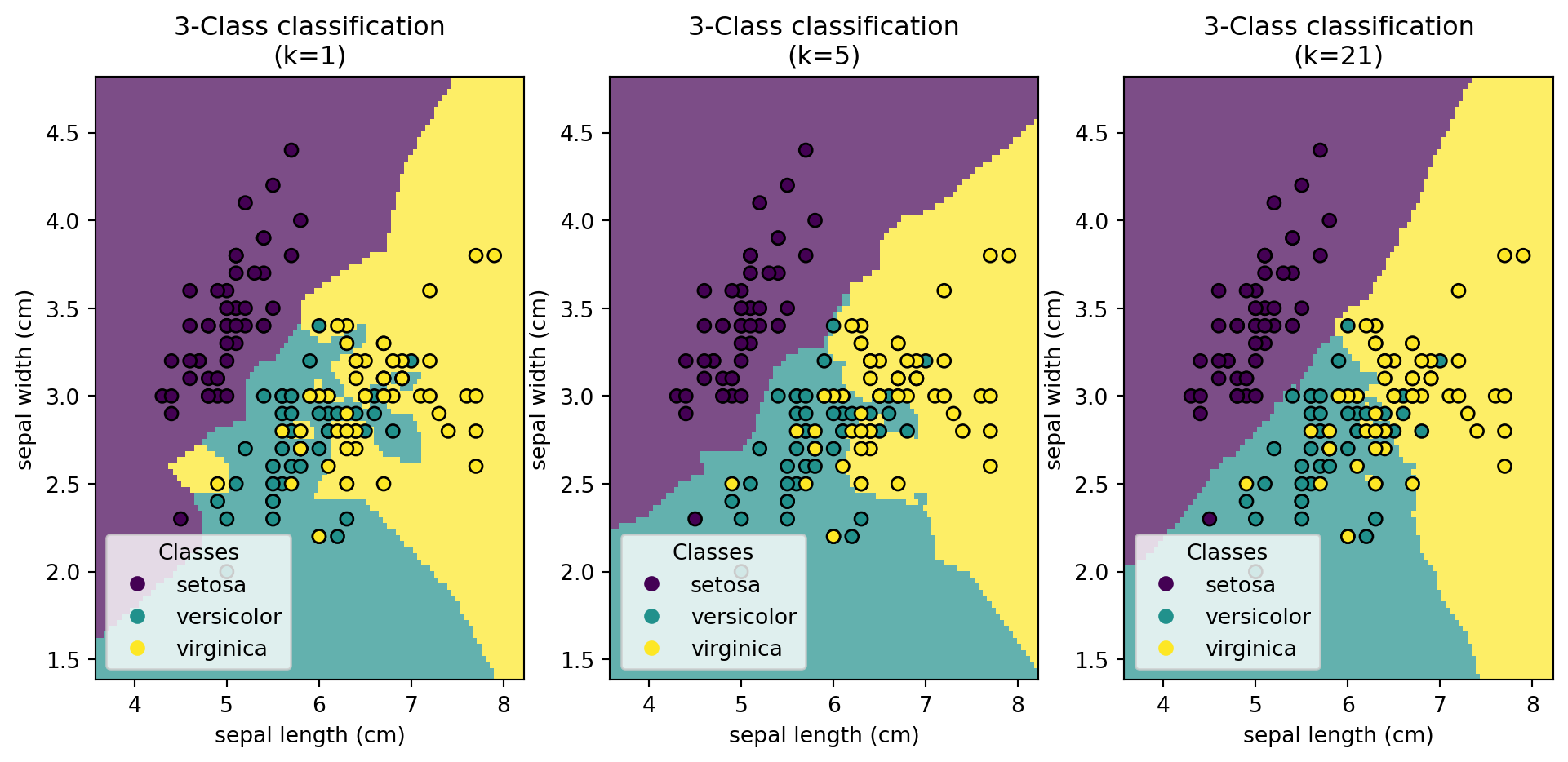
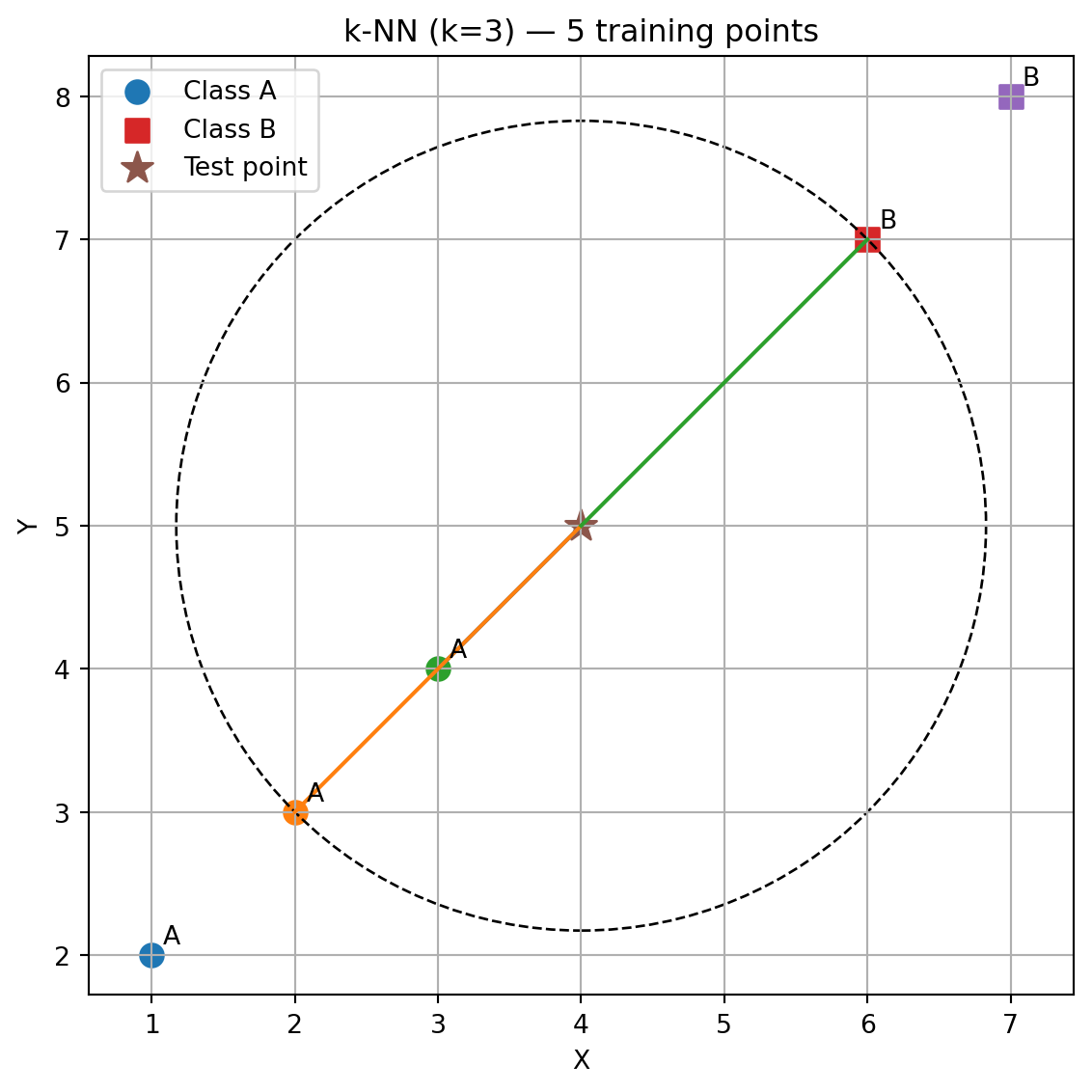
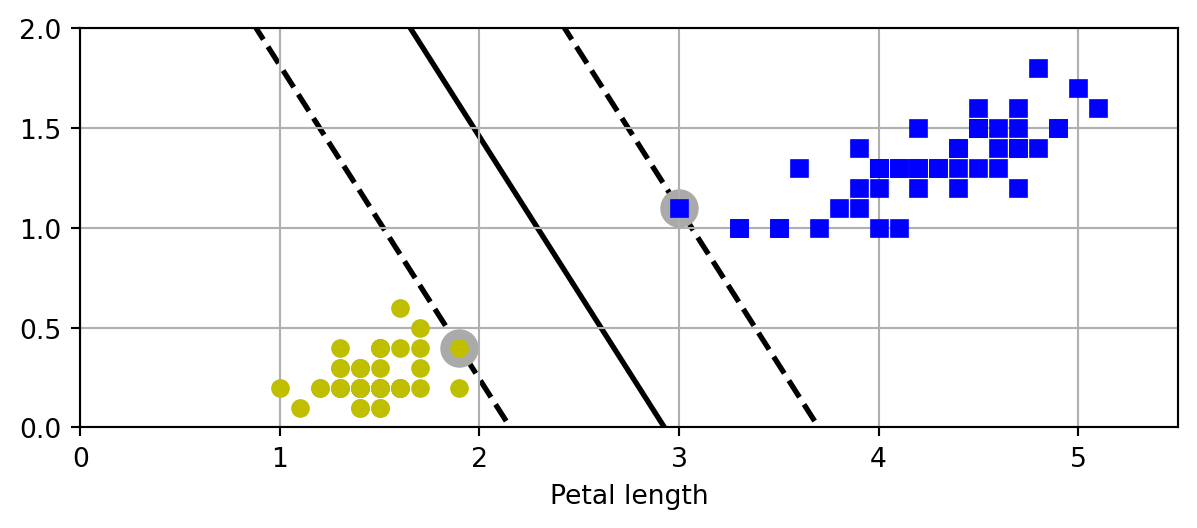
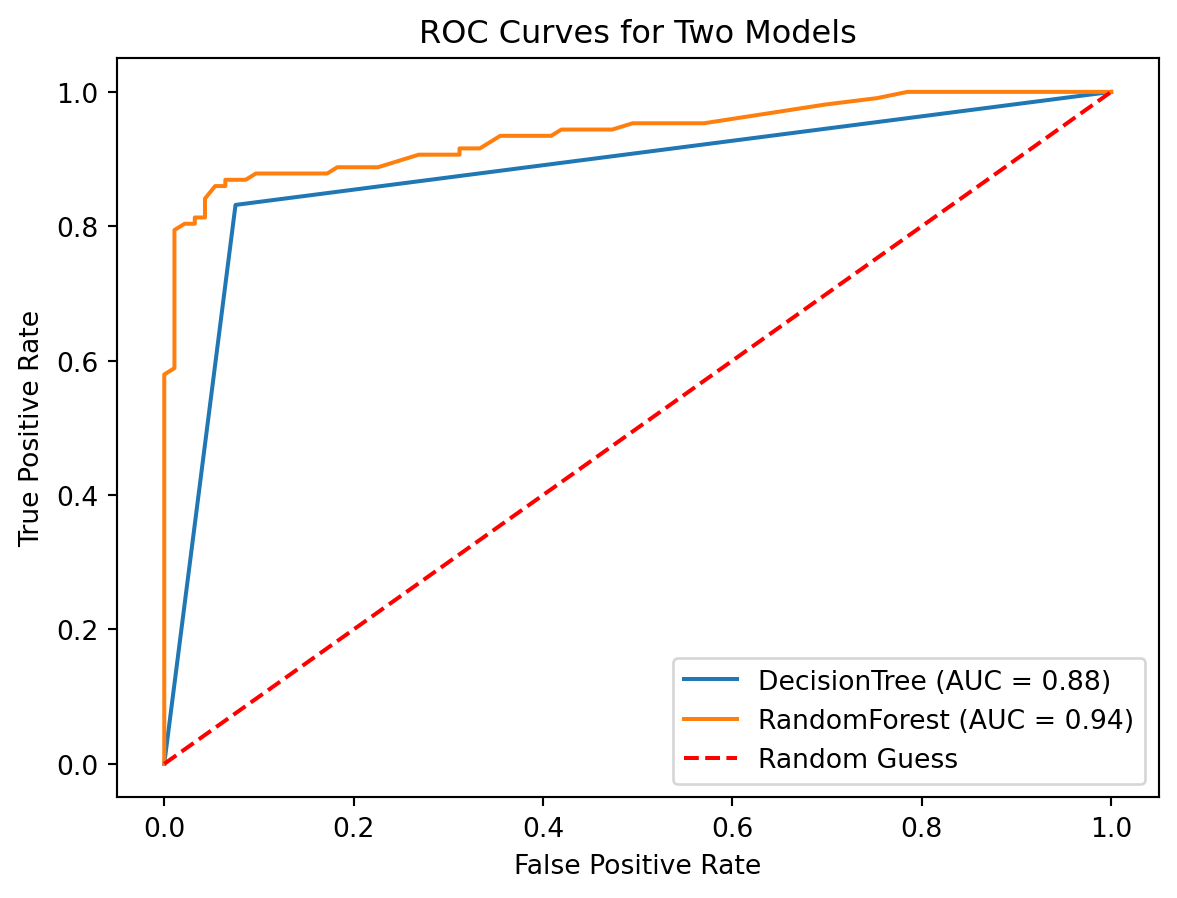
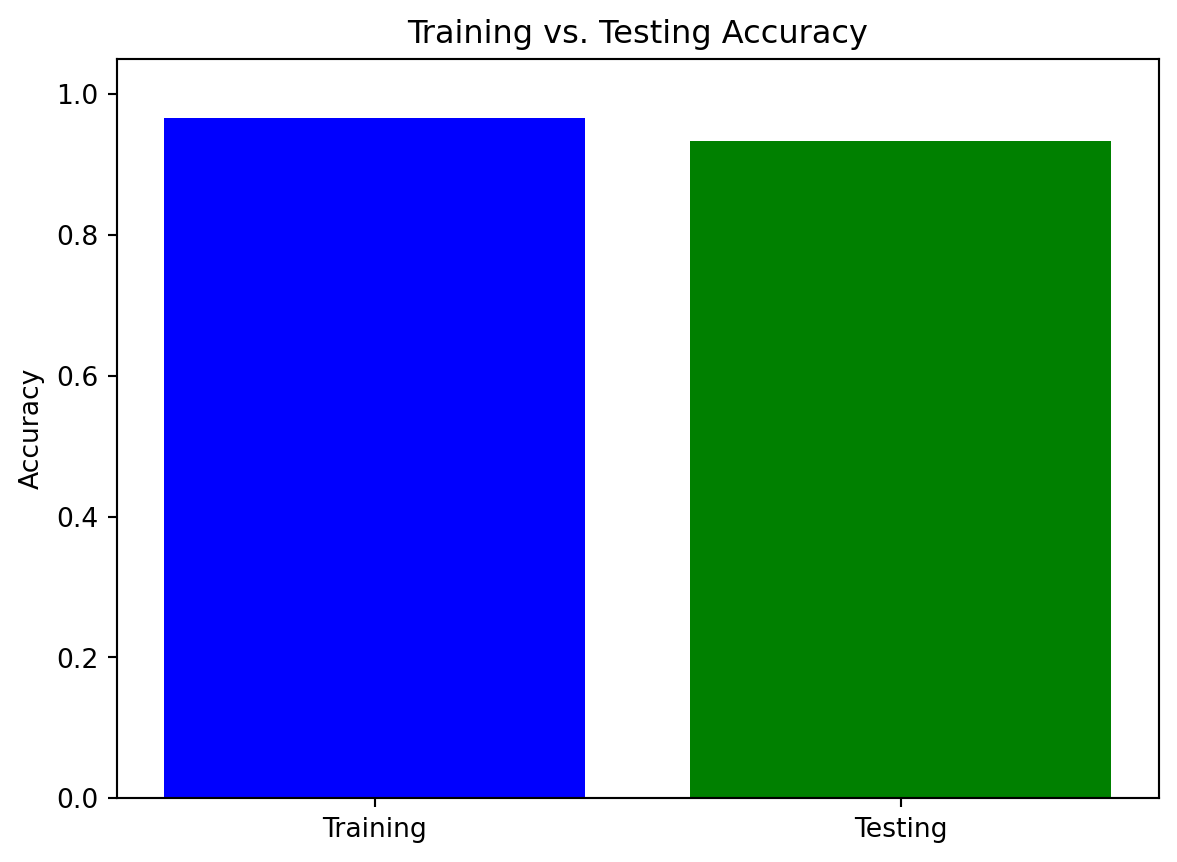
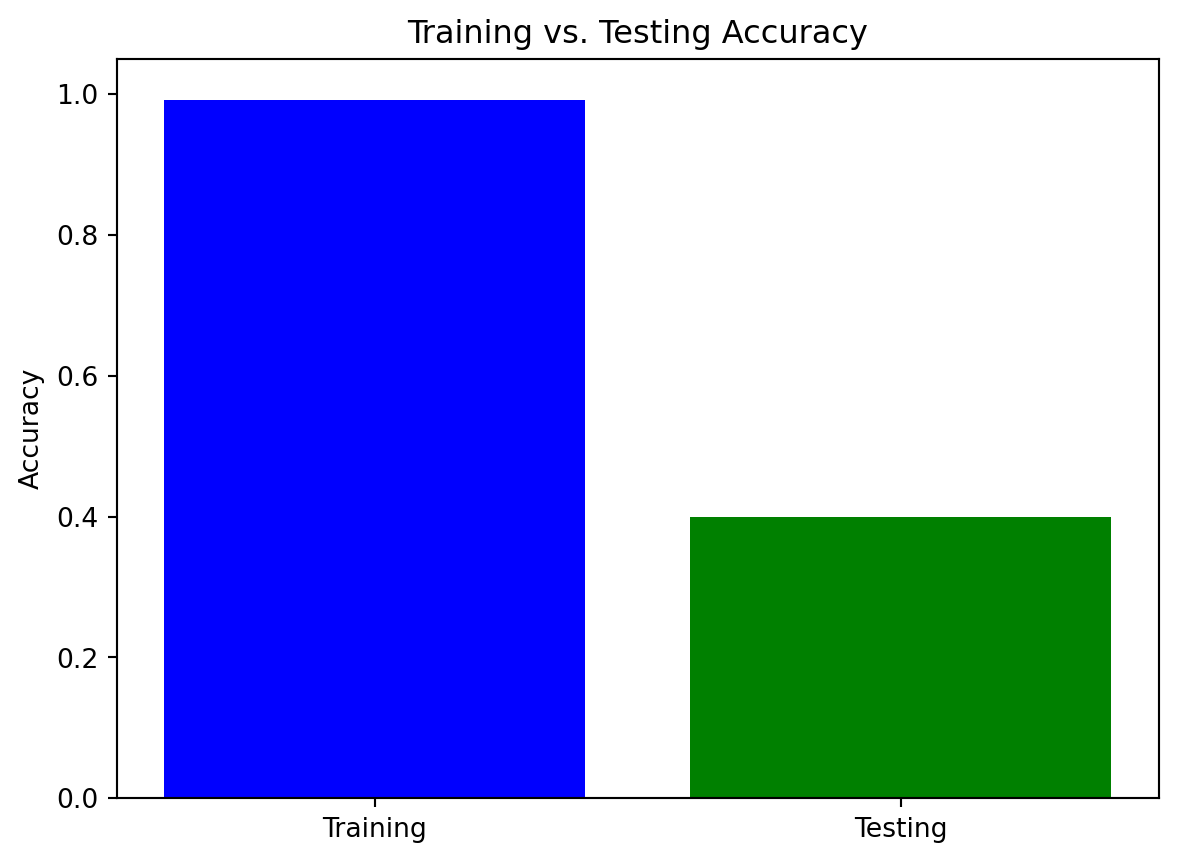
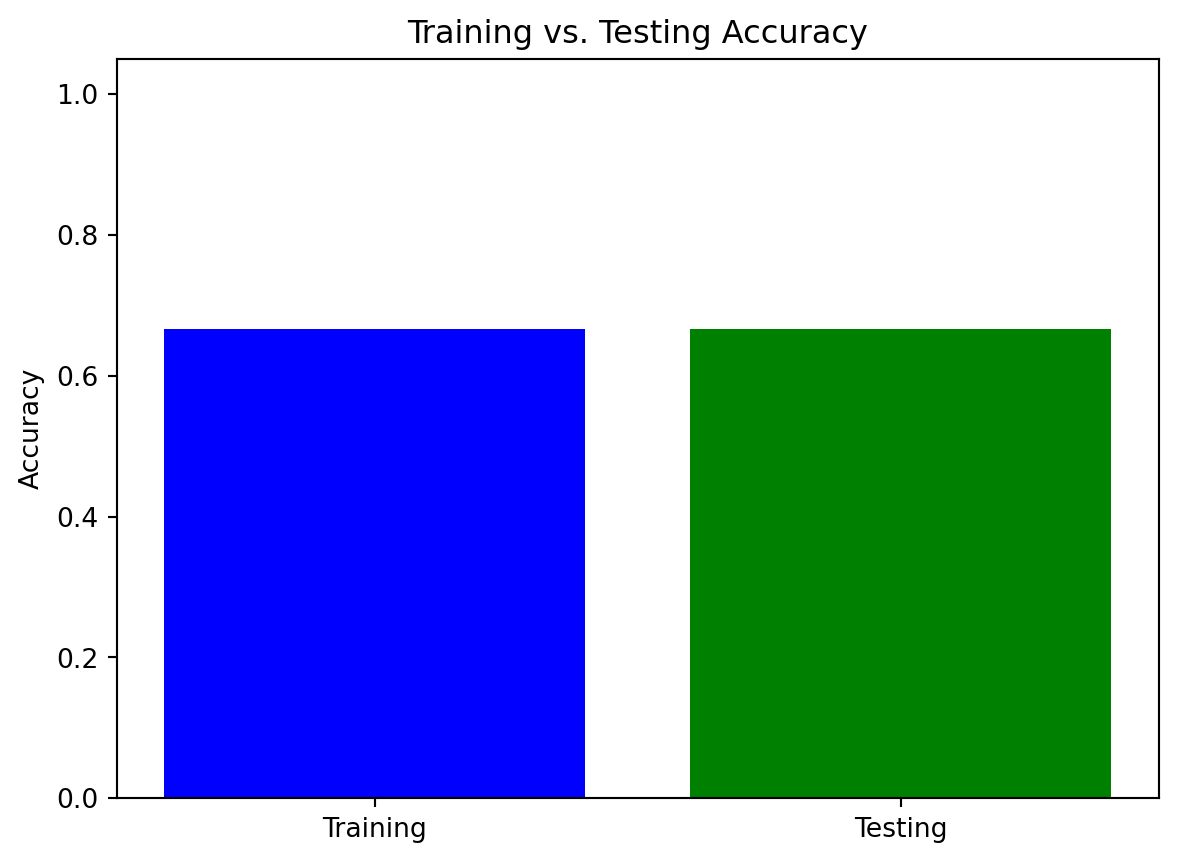
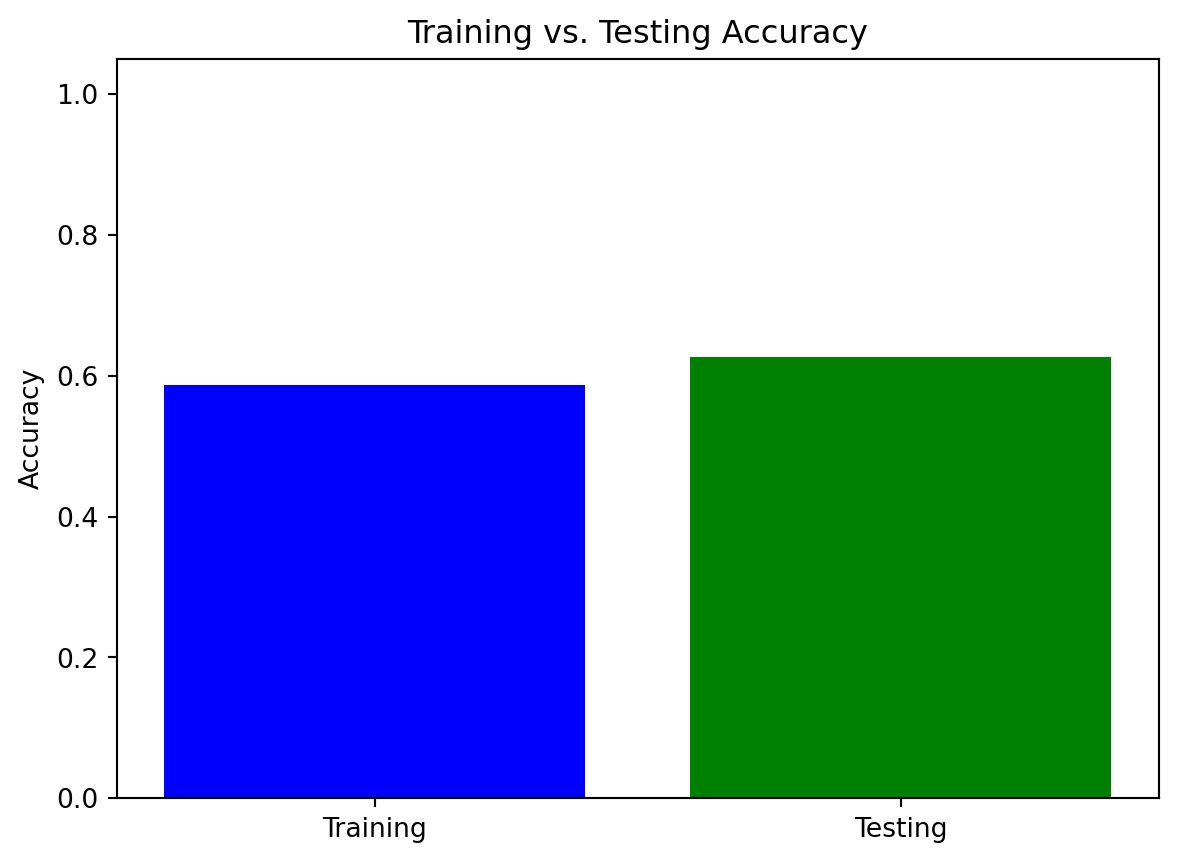
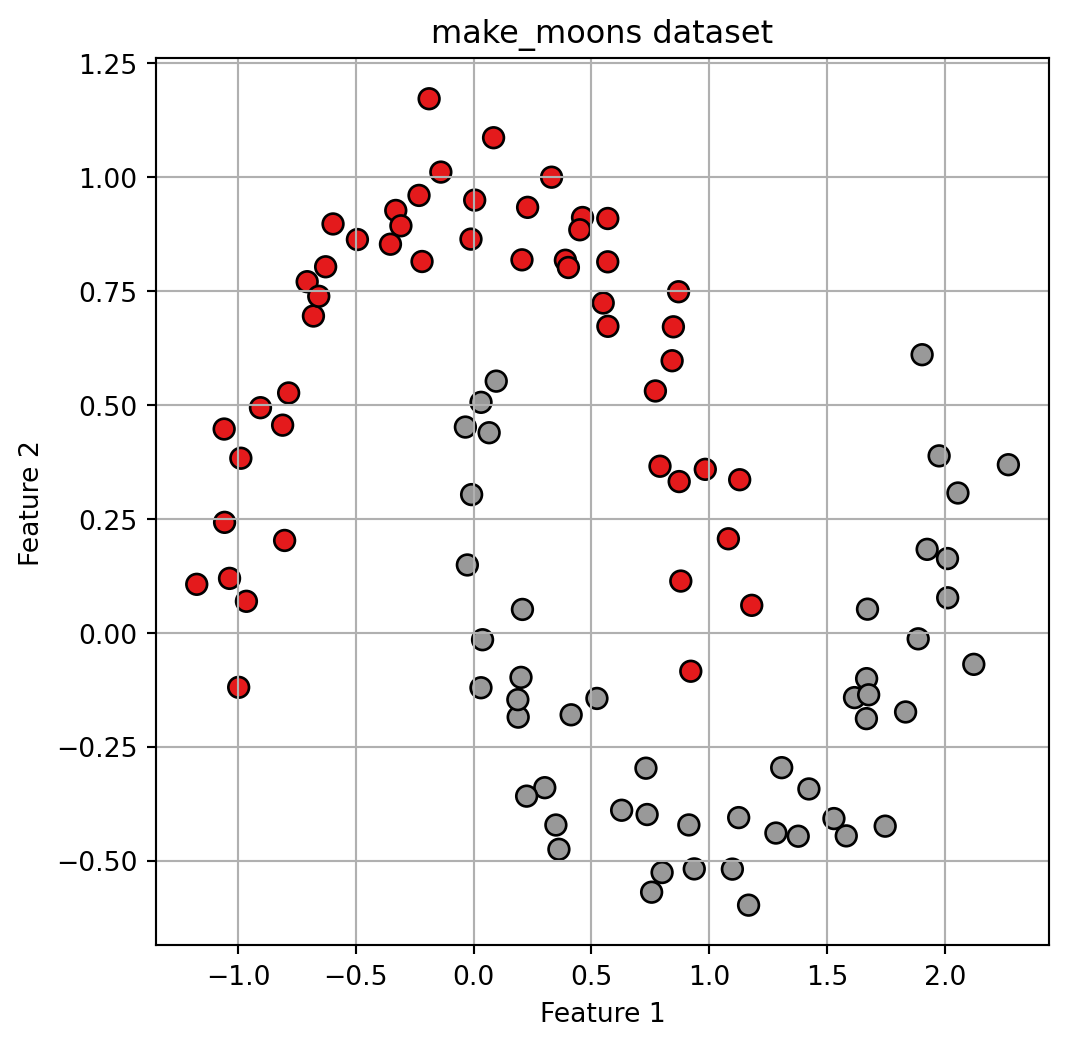
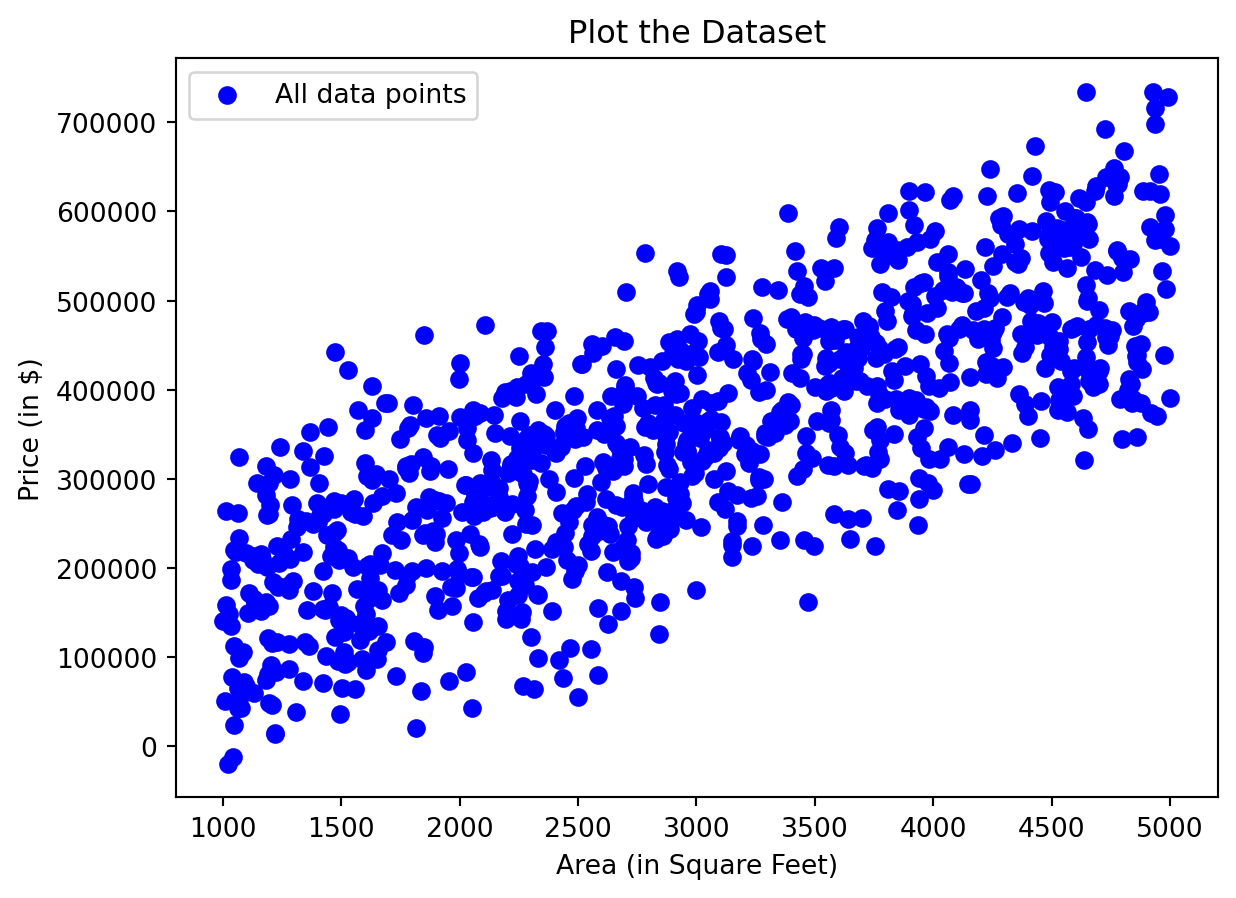
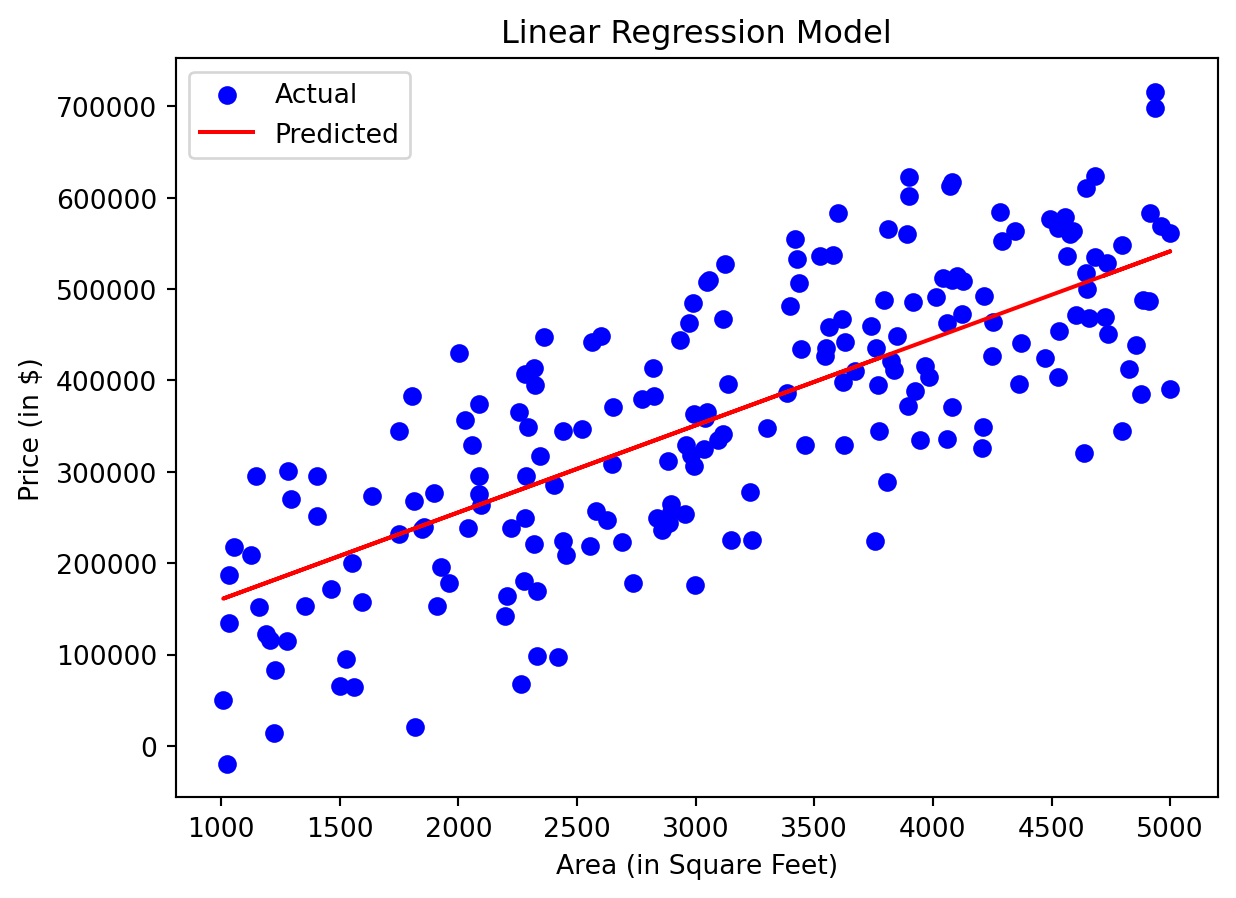
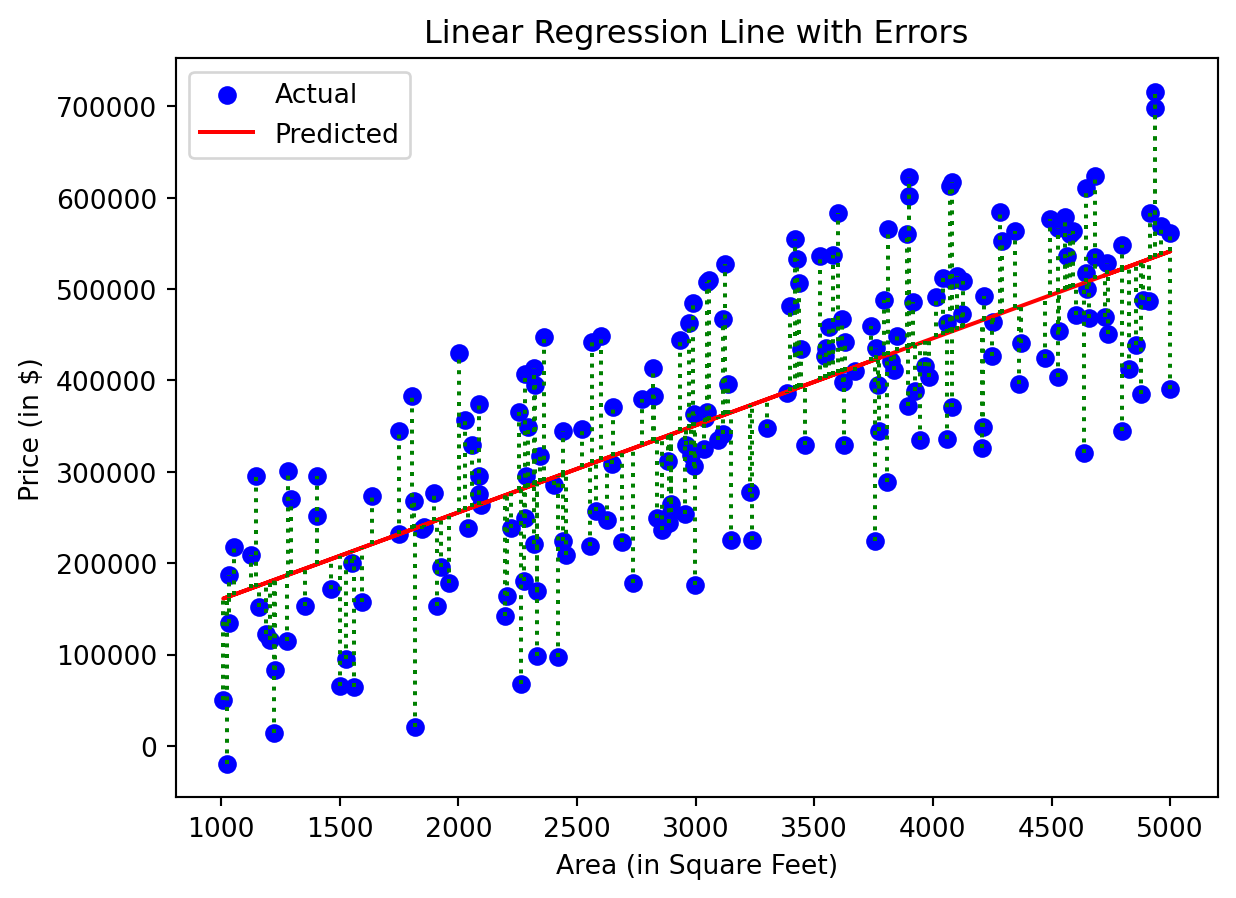
import pandas as pd
from sklearn.tree import DecisionTreeClassifier, export_text, plot_tree
import matplotlib.pyplot as plt
# Load the cat dataset mentioned in class
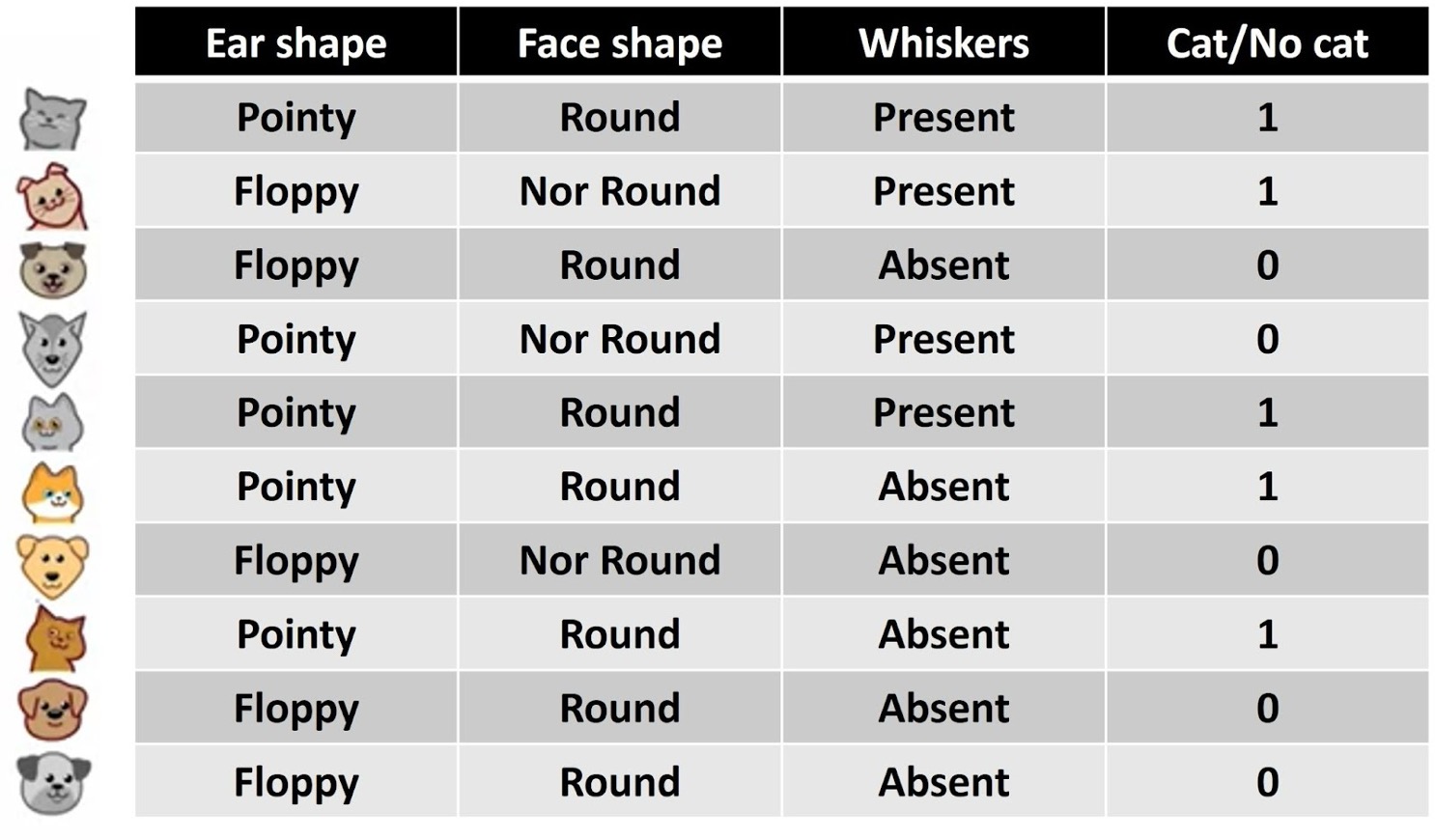
data = [
{"Ear shape":"Pointy", "Face shape":"Round", "Whiskers":"Present", "Cat/No cat":1},
{"Ear shape":"Floppy", "Face shape":"Not Round", "Whiskers":"Present", "Cat/No cat":1},
{"Ear shape":"Floppy", "Face shape":"Round", "Whiskers":"Absent", "Cat/No cat":0},
{"Ear shape":"Pointy", "Face shape":"Not Round", "Whiskers":"Present", "Cat/No cat":0},
{"Ear shape":"Pointy", "Face shape":"Round", "Whiskers":"Present", "Cat/No cat":1},
{"Ear shape":"Pointy", "Face shape":"Round", "Whiskers":"Absent", "Cat/No cat":1},
{"Ear shape":"Floppy", "Face shape":"Not Round", "Whiskers":"Absent", "Cat/No cat":0},
{"Ear shape":"Pointy", "Face shape":"Round", "Whiskers":"Absent", "Cat/No cat":1},
{"Ear shape":"Floppy", "Face shape":"Round", "Whiskers":"Absent", "Cat/No cat":0},
{"Ear shape":"Floppy", "Face shape":"Round", "Whiskers":"Absent", "Cat/No cat":0},
]
df = pd.DataFrame(data)
# Split the dataset into features (X) and target variable (y)
X = pd.get_dummies(df.drop(columns=["Cat/No cat"]))
y = df["Cat/No cat"]
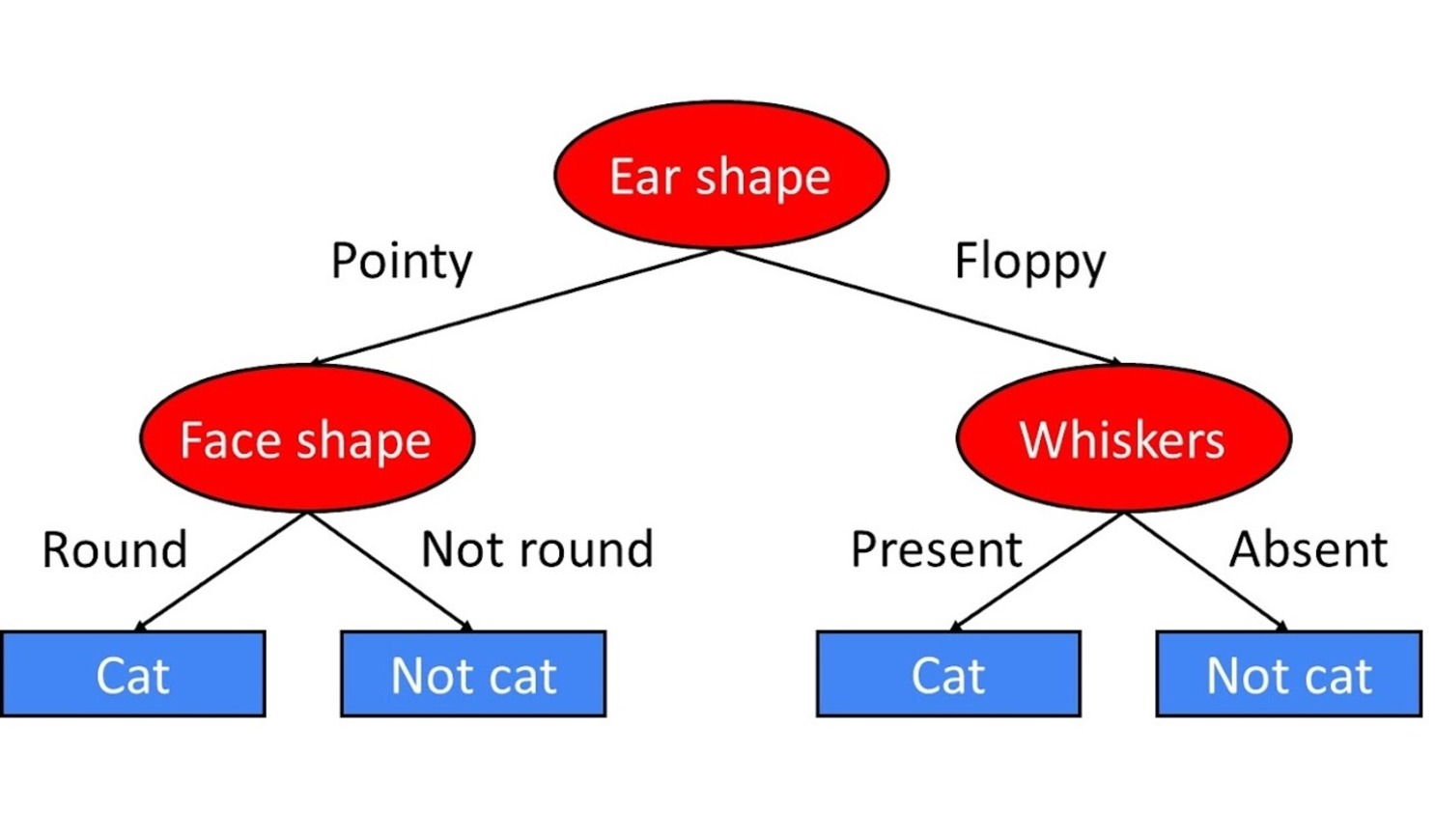
# Train our decision tree (we use entropy for IG in the sklearn library)
# Not limit the depth of the tree (max_depth=None) to allow full growth
clf = DecisionTreeClassifier(criterion="entropy", max_depth=None, random_state=0)
clf.fit(X, y)
# Show decision rules
print("Decision Tree Rules:\n")
print(export_text(clf, feature_names=list(X.columns)))
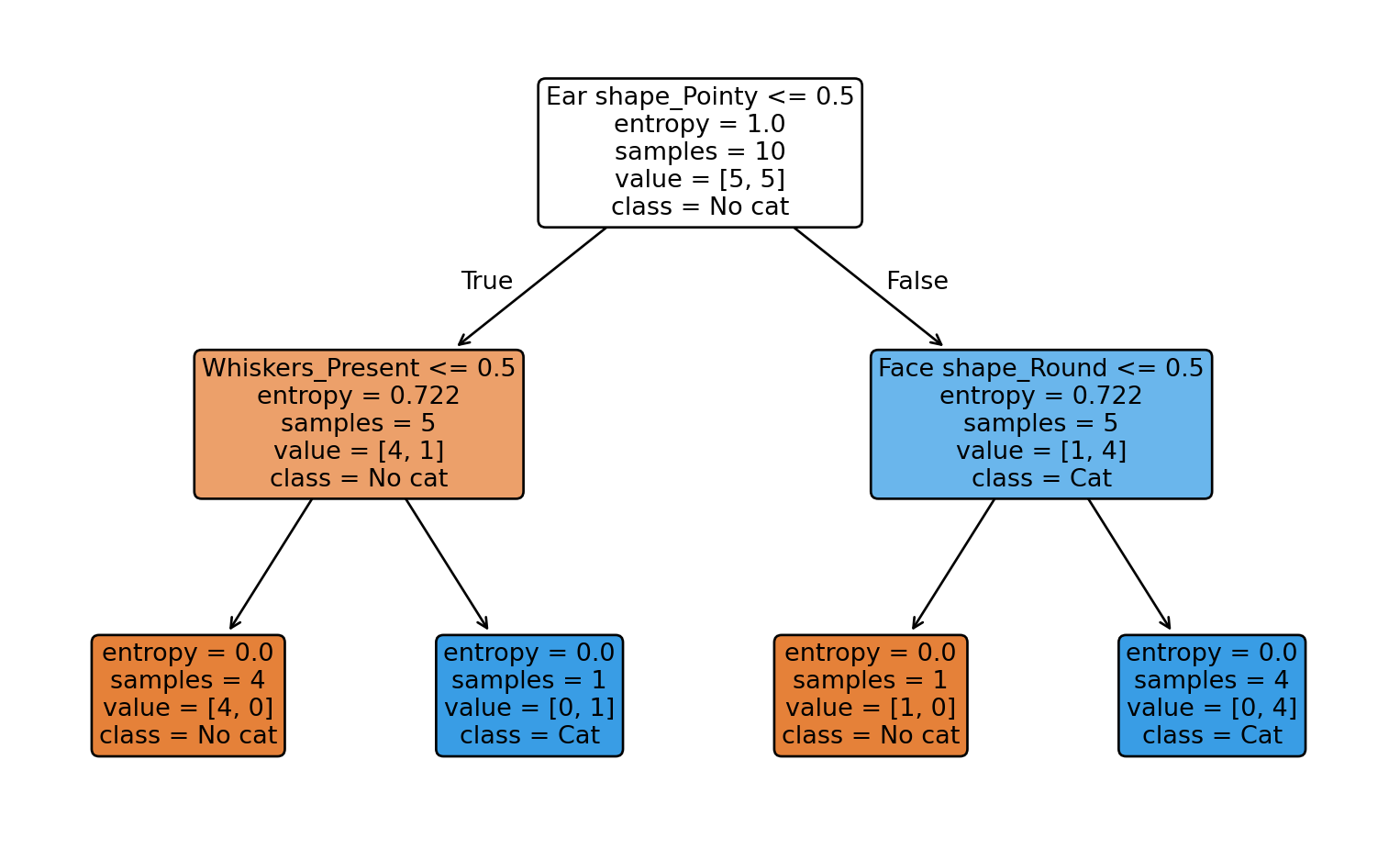
# Plot the tree use the plot_tree function
print("Decision Tree Diagram:\n")
plt.figure(figsize=(10,6))
plot_tree(clf, feature_names=X.columns, class_names=["No cat","Cat"], filled=True, rounded=True)
plt.show()Decision Tree Rules:
|--- Ear shape_Pointy <= 0.50
| |--- Whiskers_Present <= 0.50
| | |--- class: 0
| |--- Whiskers_Present > 0.50
| | |--- class: 1
|--- Ear shape_Pointy > 0.50
| |--- Face shape_Round <= 0.50
| | |--- class: 0
| |--- Face shape_Round > 0.50
| | |--- class: 1
Decision Tree Diagram:
The example below uses the KNN Classifier to classify the Iris dataset. We will visualize the decision boundary with different values of k (number of closest neighbors).
import matplotlib.pyplot as plt
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.neighbors import KNeighborsClassifier
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
iris = load_iris(as_frame=True)
X = iris.data[["sepal length (cm)", "sepal width (cm)"]]
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)
clf = Pipeline(
steps=[("scaler", StandardScaler()), ("knn", KNeighborsClassifier(weights="uniform"))]
)
_, axs = plt.subplots(ncols=3, figsize=(12, 5))
for ax, neighbors in zip(axs, (1, 5, 21)):
clf.set_params(knn__n_neighbors=neighbors).fit(X_train, y_train)
disp = DecisionBoundaryDisplay.from_estimator(
clf,
X_test,
response_method="predict",
plot_method="pcolormesh",
xlabel=iris.feature_names[0],
ylabel=iris.feature_names[1],
shading="auto",
alpha=0.7,
ax=ax,
)
scatter = disp.ax_.scatter(X.iloc[:, 0], X.iloc[:, 1], c=y, edgecolors="k")
disp.ax_.legend(
scatter.legend_elements()[0],
iris.target_names,
loc="lower left",
title="Classes",
)
_ = disp.ax_.set_title(
f"3-Class classification\n(k={clf[-1].n_neighbors})"
)
plt.show()
Given a set of training data points and their corresponding labels, the function knn_predict predicts the label for a new test point based on the majority label of its k-nearest neighbors. We use Counter function from the collections library to find the most common label among the neighbors.
import numpy as np
from collections import Counter
# Defining the Euclidean Distance Function
# euclidean_distance function is to calculate euclidean distance between points.
def euclidean_distance(point1, point2):
return np.sqrt(np.sum((np.array(point1) - np.array(point2))**2))
def knn_predict(training_data, training_labels, test_point, k):
distances = []
for i in range(len(training_data)):
dist = euclidean_distance(test_point, training_data[i])
distances.append((dist, training_labels[i]))
distances.sort(key=lambda x: x[0])
k_nearest_labels = [label for _, label in distances[:k]]
return Counter(k_nearest_labels).most_common(1)[0][0]
training_data = [[1, 2], [2, 3], [3, 4], [6, 7], [7, 8]]
training_labels = ['A', 'A', 'A', 'B', 'B']
test_point = [4, 5]
k = 3 # Number of the closest neighbors to consider
prediction = knn_predict(training_data, training_labels, test_point, k)
print(f"The predicted class for the test point is: {prediction}")The predicted class for the test point is: APlot the decision boundary of the KNN classifier implemented from scratch.
Q1: Will you like a movie? Please classify the following movies using Decision Tree Classifier taught in the class.
| Movie | Type | Length | IMDb Rating | Liked? |
|---|---|---|---|---|
| m1 | Comedy | Short | 7.2 | Yes |
| m2 | Drama | Medium | 9.3 | Yes |
| m3 | Comedy | Medium | 5.1 | No |
| m4 | Drama | Long | 6.9 | No |
| m5 | Drama | Medium | 8.3 | Yes |
| m6 | Drama | Short | 4.5 | No |
| m7 | Comedy | Short | 8.0 | Yes |
| m8 | Drama | Medium | 7.5 | Yes |
Q2: Suppose we have height, weight and T-shirt size of some customers and we need to predict the T-shirt size of a new customer given only height and weight information we have. Data including height, weight and T-shirt size information is shown in the table below. New customer named ‘Monica’ has height 161cm and weight 61kg. Can you use KNN Classifier to predict Monica’s T-shirt size? k is set to be 5 in this example.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Height (cms) | 158 | 158 | 158 | 160 | 160 | 163 | 163 | 160 | 163 | 165 | 165 | 165 | 168 | 168 | 168 | 170 | 170 | 170 |
| Weight (kgs) | 58 | 59 | 63 | 59 | 60 | 60 | 61 | 64 | 64 | 61 | 62 | 65 | 62 | 63 | 66 | 63 | 64 | 68 |
| T-Shirt Size | M | M | M | M | M | M | M | L | L | L | L | L | L | L | L | L | L | L |
The example below uses the SVM Classifier to classify the Iris dataset (setosa or versicolor). We will visualize the SVM decision boundary in the plot.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.svm import SVC
from sklearn import datasets
# Load the Iris dataset
iris = datasets.load_iris(as_frame=True)
X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = iris.target
setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
# Train the SVM Classifier
svm_clf = SVC(kernel="linear", C=1e100) # C is a Regularization Parameter
svm_clf.fit(X, y)
def plot_svc_decision_boundary(svm_clf, xmin, xmax):
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
# At the decision boundary, w0*x0 + w1*x1 + b = 0
# => x1 = -w0/w1 * x0 - b/w1
x0 = np.linspace(xmin, xmax, 200)
decision_boundary = -w[0] / w[1] * x0 - b / w[1]
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
svs = svm_clf.support_vectors_
plt.plot(x0, decision_boundary, "k-", linewidth=2, zorder=-2)
plt.plot(x0, gutter_up, "k--", linewidth=2, zorder=-2)
plt.plot(x0, gutter_down, "k--", linewidth=2, zorder=-2)
plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#AAA',
zorder=-1)
fig, axes = plt.subplots(ncols=1, figsize=(10, 2.7), sharey=True)
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.xlabel("Petal length")
plt.axis([0, 5.5, 0, 2])
plt.gca().set_aspect("equal")
plt.grid()
plt.show()
Q1: Consider the car theft problem with attributes Color, Type, Origin, and the target, Stolen can be either Yes or No. Please Use the Naive Bayes Classifier to solve the following problems.
| Example No. | Color | Type | Origin | Stolen? |
|---|---|---|---|---|
| 1 | Red | Sports | Domestic | Yes |
| 2 | Red | Sports | Domestic | No |
| 3 | Red | Sports | Domestic | Yes |
| 4 | Yellow | Sports | Domestic | No |
| 5 | Yellow | Sports | Imported | Yes |
| 6 | Yellow | SUV | Imported | No |
| 7 | Yellow | SUV | Imported | Yes |
| 8 | Yellow | SUV | Domestic | No |
| 9 | Red | SUV | Imported | No |
| 10 | Red | Sports | Imported | Yes |
Q1.1: What is the possibilty of a Red SUV Domestic car being stolen?
Q1.2: What is the possibilty of a Red SUV Domestic car Not being stolen?
Q1.3: Given the possibilites, do you think the Red SUV Domestic car will be stolen or not?
Q2: Could you use Support Vector Machine (SVM) to predict a Pulsar Star? The dataset can be downloaded here. Pulsars are a rare type of Neutron star that produce radio emission detectable here on Earth. They are of considerable scientific interest as probes of space-time, the inter-stellar medium, and states of matter. Classification algorithms in particular are being adopted, which treat the data sets as binary classification problems. Here the legitimate pulsar examples form minority positive class and spurious examples form the majority negative class. The dataset here contains 16,259 spurious examples caused by RFI/noise, and 1,639 real pulsar examples. Each row lists the variables first, and the class label is the final entry. The class labels used are 0 (negative) and 1 (positive).
Attribute Information: Each candidate is described by 8 continuous variables, and a single class variable. The first four are simple statistics obtained from the integrated pulse profile. The remaining four variables are similarly obtained from the DM-SNR curve . These are summarised below:
Example code is provided below for references (contain data preprocessing). The code below only prepares the data. You need to add code for SVM model training and prediction after the data preparation part. We aim to run SVM with default hyperparameters. The model prediction accuracy should be 0.9827 at the end. Note that if you do not have a Python IDE set up, you can run the following code in Google Colab.
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
from sklearn.model_selection import train_test_split # Split the dataset into training and testing sets
from sklearn.preprocessing import StandardScaler # Feature scaling
df = pd.read_csv("pulsar_stars.csv")
print(f"Dataset shape: {df.shape}")
# let's preview the dataset
# print(df.head(5))
print(f"Column names: {df.columns.str.strip()}")
# view summary of dataset
# print(f"Dataset summary:\n{df.describe()}")
X = df.drop(['target_class'], axis=1) # Drop specified labels from rows or columns.
y = df['target_class']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
print(f"Training set shape: {X_train.shape}, Test set shape: {X_test.shape}")
# Feature Scaling
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# Construct DataFrames
X_train = pd.DataFrame(X_train, columns=X.columns)
X_test = pd.DataFrame(X_test, columns=X.columns)
# After data preparation, we now run SVM with default hyperparameters
# Code for SVM model training and evaluation goes below ⬇️Dataset shape: (17898, 9)
Column names: Index(['Mean of the integrated profile',
'Standard deviation of the integrated profile',
'Excess kurtosis of the integrated profile',
'Skewness of the integrated profile', 'Mean of the DM-SNR curve',
'Standard deviation of the DM-SNR curve',
'Excess kurtosis of the DM-SNR curve', 'Skewness of the DM-SNR curve',
'target_class'],
dtype='object')
Training set shape: (14318, 8), Test set shape: (3580, 8)The ROC curve is a graphical representation of the performance of a binary classifier system as its discrimination threshold is varied. It plots the True Positive Rate (TPR) against the False Positive Rate (FPR) at various threshold settings.
AUC is a single scalar value that summarizes the overall performance of the classifier across all possible thresholds. The AUC value ranges from 0 to 1, where a value of 1 indicates perfect classification and a value of 0.5 indicates random guessing. Trapezoidal Rule is used to calculate the area under the ROC curve.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_curve, auc
# Generate a synthetic binary classification dataset
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
decision_tree_model = DecisionTreeClassifier(random_state=42)
decision_tree_model.fit(X_train, y_train)
y_pred_tree = decision_tree_model.predict_proba(X_test)[:, 1]
random_forest_model = RandomForestClassifier(n_estimators=100, random_state=42)
random_forest_model.fit(X_train, y_train)
y_pred_rf = random_forest_model.predict_proba(X_test)[:, 1]
# Create a DataFrame to store the true/positive labels and predicted probabilities for both models
test_df = pd.DataFrame({'True': y_test, 'DecisionTree': y_pred_tree, 'RandomForest': y_pred_rf})
plt.figure(figsize=(7, 5))
for model in ['DecisionTree', 'RandomForest']:
fpr, tpr, _ = roc_curve(test_df['True'], test_df[model])
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, label=f'{model} (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], 'r--', label='Random Guess')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curves for Two Models')
plt.legend()
plt.show()
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, KFold, cross_val_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, confusion_matrix
data = load_iris()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)
tree = DecisionTreeClassifier(criterion="entropy",
max_depth=3,
min_samples_leaf=5,
random_state=42)
tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
train_acc = accuracy_score(y_train, y_train_pred)
test_acc = accuracy_score(y_test, y_test_pred)
print(f"Training Accuracy: {train_acc:.4f}")
print(f"Testing Accuracy: {test_acc:.4f}")
cm = confusion_matrix(y_test, y_test_pred)
cm_df = pd.DataFrame(cm,
index=[f"Actual {label}" for label in data.target_names],
columns=[f"Predicted {label}" for label in data.target_names])
print("\nConfusion Matrix (test data):")
print(cm_df)
plt.bar(["Training", "Testing"], [train_acc, test_acc], color=["blue", "green"])
plt.ylim(0, 1.05)
plt.ylabel("Accuracy")
plt.title("Training vs. Testing Accuracy")
plt.show()Training Accuracy: 0.9667
Testing Accuracy: 0.9333
Confusion Matrix (test data):
Predicted setosa Predicted versicolor Predicted virginica
Actual setosa 10 0 0
Actual versicolor 0 9 1
Actual virginica 0 1 9
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, KFold, cross_val_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, confusion_matrix
data = load_iris()
X, y = data.data, data.target
# Add noise to magnify overfitting behavior
noise_rate = 0.40
rng = np.random.RandomState(42)
if noise_rate > 0:
n_flip = int(noise_rate * len(y))
idx = rng.choice(len(y), size=n_flip, replace=False)
for i in idx:
choices = [c for c in np.unique(y) if c != y[i]]
y[i] = rng.choice(choices)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)
tree = DecisionTreeClassifier(criterion="entropy",
max_depth=None,
min_samples_leaf=1,
min_samples_split=2,
random_state=42)
tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
train_acc = accuracy_score(y_train, y_train_pred)
test_acc = accuracy_score(y_test, y_test_pred)
print(f"Training Accuracy: {train_acc:.4f}")
print(f"Testing Accuracy: {test_acc:.4f}")
cm = confusion_matrix(y_test, y_test_pred)
cm_df = pd.DataFrame(cm,
index=[f"Actual {label}" for label in data.target_names],
columns=[f"Predicted {label}" for label in data.target_names])
print("\nConfusion Matrix (test data):")
print(cm_df)
plt.bar(["Training", "Testing"], [train_acc, test_acc], color=["blue", "green"])
plt.ylim(0, 1.05)
plt.ylabel("Accuracy")
plt.title("Training vs. Testing Accuracy")
plt.show()Training Accuracy: 0.9917
Testing Accuracy: 0.4000
Confusion Matrix (test data):
Predicted setosa Predicted versicolor Predicted virginica
Actual setosa 3 3 3
Actual versicolor 2 5 4
Actual virginica 3 3 4
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, StratifiedKFold, cross_val_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, confusion_matrix
data = load_iris()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)
tree = DecisionTreeClassifier(criterion="entropy",
max_depth=1,
min_samples_leaf=20,
random_state=42)
tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
train_acc = accuracy_score(y_train, y_train_pred)
test_acc = accuracy_score(y_test, y_test_pred)
print(f"Training Accuracy: {train_acc:.4f}")
print(f"Testing Accuracy: {test_acc:.4f}")
cm = confusion_matrix(y_test, y_test_pred)
cm_df = pd.DataFrame(cm,
index=[f"Actual {label}" for label in data.target_names],
columns=[f"Predicted {label}" for label in data.target_names])
print("\nConfusion Matrix (test):")
print(cm_df)
plt.bar(["Training", "Testing"], [train_acc, test_acc], color=["blue", "green"])
plt.ylim(0, 1.05)
plt.ylabel("Accuracy")
plt.title("Training vs. Testing Accuracy")
plt.show()Training Accuracy: 0.6667
Testing Accuracy: 0.6667
Confusion Matrix (test):
Predicted setosa Predicted versicolor Predicted virginica
Actual setosa 10 0 0
Actual versicolor 0 10 0
Actual virginica 0 10 0
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, RepeatedStratifiedKFold, cross_val_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, confusion_matrix
data = load_iris()
X, y = data.data, data.target
# Add noise
rng = np.random.RandomState(42)
noise_rate = 0.15
n_flip = int(noise_rate * len(y))
idx = rng.choice(len(y), size=n_flip, replace=False)
for i in idx:
choices = [c for c in np.unique(y) if c != y[i]]
y[i] = rng.choice(choices)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=42, stratify=y)
tree = DecisionTreeClassifier(criterion="entropy",
max_depth=1,
min_samples_leaf=5,
random_state=42)
tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
train_acc = accuracy_score(y_train, y_train_pred)
test_acc = accuracy_score(y_test, y_test_pred)
print(f"Training Accuracy: {train_acc:.4f}")
print(f"Testing Accuracy: {test_acc:.4f}")
cm = confusion_matrix(y_test, y_test_pred)
cm_df = pd.DataFrame(cm,
index=[f"Actual {label}" for label in data.target_names],
columns=[f"Predicted {label}" for label in data.target_names])
print("\nConfusion Matrix (test):")
print(cm_df)
plt.bar(["Training", "Testing"], [train_acc, test_acc], color=["blue", "green"])
plt.ylim(0, 1.05)
plt.ylabel("Accuracy")
plt.title("Training vs. Testing Accuracy")
plt.show()Training Accuracy: 0.5867
Testing Accuracy: 0.6267
Confusion Matrix (test):
Predicted setosa Predicted versicolor Predicted virginica
Actual setosa 23 0 4
Actual versicolor 1 0 21
Actual virginica 2 0 24
In this example, we will train a decision tree classification model on telecom customer churn dataset and use different ensemble methods (bagging, boosting, and stacking) to improve the performance. We will use a free open-source dataset to run our code.
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import StackingClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, cross_val_score
# Load the telecom customer churn dataset from a CSV file
customer = pd.read_csv("customer_churn.csv")
customer.head()
X = customer.drop("Churn", axis=1)
y = customer.Churn
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)
# Training the model using the predefined pipeline from sklearn library
pipeline = Pipeline([('scaler', StandardScaler()),
('classifier', DecisionTreeClassifier(random_state=42))])
pipeline.fit(X_train, y_train)
# Evaluate the decision tree classifier using cross-validation
cv_scores = cross_val_score(pipeline, X, y, cv=5)
print("Simple Decision Tree Classifier Results:")
print(f"Cross-validation scores: {cv_scores}")
print(f"Mean CV accuracy: {np.mean(cv_scores):.2f}")
# Bagging Classifier
bagging_classifier = BaggingClassifier(estimator=pipeline,
n_estimators=50,
random_state=42)
bagging_classifier.fit(X_train, y_train)
cv_scores = cross_val_score(bagging_classifier, X, y, cv=5)
print("\nBagging Classifier Results:")
print(f"Cross-validation scores: {cv_scores}")
print(f"Mean CV accuracy: {np.mean(cv_scores):.2f}")
# Adaboost Classifier
base_tree = DecisionTreeClassifier(max_depth=1, random_state=42)
adaboost_classifier = AdaBoostClassifier(estimator=base_tree,
n_estimators=50,
random_state=42)
adaboost_classifier.fit(X_train, y_train)
cv_scores = cross_val_score(adaboost_classifier, X, y, cv=5)
print("\nAdaBoost Classifier Results:")
print(f"Cross-validation scores: {cv_scores}")
print(f"Mean CV accuracy: {np.mean(cv_scores):.2f}")
# Stacking Classifier
stacking_classifier = StackingClassifier(estimators=[('bagging', bagging_classifier),
('adaboost', adaboost_classifier)],
final_estimator=DecisionTreeClassifier(random_state=42))
stacking_classifier.fit(X_train, y_train)
cv_scores = cross_val_score(stacking_classifier, X, y, cv=5)
print("\nStacking Classifier Results:")
print(f"Cross-validation scores: {cv_scores}")
print(f"Mean CV accuracy: {np.mean(cv_scores):.2f}")Simple Decision Tree Classifier Results:
Cross-validation scores: [0.9 0.55 0.95 0.8 0.35]
Mean CV accuracy: 0.71
Bagging Classifier Results:
Cross-validation scores: [0.85 0.85 0.95 0.9 0.8 ]
Mean CV accuracy: 0.87
AdaBoost Classifier Results:
Cross-validation scores: [0.85 0.75 0.95 0.8 0.7 ]
Mean CV accuracy: 0.81
Stacking Classifier Results:
Cross-validation scores: [0.9 0.7 0.85 0.85 0.85]
Mean CV accuracy: 0.83Q1: Can you use the ensemble learning methods (bagging, boosting, and stacking) to improve the performance of a decision tree classifier on the make_moons dataset? Please follow the example provided above to implement your solution.
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.1, random_state=42)
# Visualize the make_moons dataset features
plt.figure(figsize=(6, 6))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1, edgecolor='k', s=60)
plt.title("make_moons dataset")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.grid(True)
plt.show()
Simple Decision Tree Classifier Results:
Cross-validation scores: [0.95 0.95 0.75 1. 0.75]
Mean CV accuracy: 0.88
Bagging Classifier Results:
Cross-validation scores: [0.95 1. 0.8 1. 0.8 ]
Mean CV accuracy: 0.91
AdaBoost Classifier Results:
Cross-validation scores: [1. 1. 0.8 1. 0.95]
Mean CV accuracy: 0.95
Stacking Classifier Results:
Cross-validation scores: [1. 0.95 0.75 0.95 0.95]
Mean CV accuracy: 0.92import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.model_selection import train_test_split
# Load the dataset
df = pd.read_csv("house-prices.csv")
# Features and target
X = df["area"].values.reshape(-1, 1) # Reshape for sklearn model
y = df["price"]
# Visualize the data
plt.figure()
plt.scatter(X, y, color="blue", label="All data points")
plt.xlabel("Area (in Square Feet)")
plt.ylabel("Price (in $)")
plt.legend()
plt.title("Plot the Dataset")
# Split the dataset into 80% for training and 20% for testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Train the model
reg_model = linear_model.LinearRegression()
reg_model.fit(X_train, y_train)
# Predict on test data
y_pred = reg_model.predict(X_test)
# Visualize the results/predictions
plt.figure()
plt.scatter(X_test, y_test, color="blue", label="Actual")
plt.plot(X_test, y_pred, color="red", label="Predicted")
plt.xlabel("Area (in Square Feet)")
plt.ylabel("Price (in $)")
plt.legend()
plt.title("Linear Regression Model")
# Visualize the errors
plt.figure()
plt.scatter(X_test, y_test, color="blue", label="Actual")
plt.plot(X_test, y_pred, color="red", label="Predicted")
X_vals = np.array(X_test).flatten()
y_true = np.array(y_test)
y_pred = np.array(y_pred)
for i in range(len(X_vals)):
plt.vlines(x=X_vals[i], ymin=min(y_true[i], y_pred[i]),
ymax=max(y_true[i], y_pred[i]), color="green",
linestyle="dotted")
plt.xlabel("Area (in Square Feet)")
plt.ylabel("Price (in $)")
plt.legend()
plt.title("Linear Regression Line with Errors")
plt.show()
import numpy as np
import matplotlib.pyplot as plt
class LogisticRegression():
def __init__(self):
self.coef_ = None
self.intercept = None
def sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def cost_function(self, X, y, weights):
"""
Computes the cost/loss function based on the cross entropy:
Cost = -1/m * Σ [y * log(ŷ) + (1 - y) * log(1 - ŷ)]
"""
z = np.dot(X, weights)
predict_1 = y * np.log(self.sigmoid(z))
predict_2 = (1 - y) * np.log(1 - self.sigmoid(z))
return -sum(predict_1 + predict_2) / len(X)
def fit(self, X, y, lr=0.01, n_iters=1000):
X = np.c_[np.ones((X.shape[0], 1)), X]
# Initialize random weights
self.weights = np.random.rand(X.shape[1])
losses = []
for _ in range(n_iters):
z = np.dot(X, self.weights)
y_hat = self.sigmoid(z)
gradient = np.dot(X.T, (y_hat - y)) / len(y)
self.weights -= lr * gradient
loss = self.cost_function(X, y, self.weights)
losses.append(loss)
return losses
def predict(self, X):
"""
Makes predictions using the trained logistic regression model. Typically set the threshold to 0.5.
Returns 1 if the probability is greater than 0.5, else 0.
"""
X = np.c_[np.ones((X.shape[0], 1)), X]
z = np.dot(X, self.weights)
predictions = self.sigmoid(z)
return [1 if i > 0.5 else 0 for i in predictions]
LogisticRegressionModel = LogisticRegression()
X = np.array([[0.5, 1.5], [1.0, 1.0], [1.5, 0.5],
[3.0, 3.5], [3.5, 3.0], [4.0, 4.0]])
y = np.array([0, 0, 0, 1, 1, 1])
# Train and get losses
losses = LogisticRegressionModel.fit(X, y, lr=0.1, n_iters=1000)
# Plot loss over iterations
plt.plot(range(len(losses)), losses)
plt.title("Cost Function over Iterations")
plt.xlabel("Iterations")
plt.ylabel("Cost")
plt.show()
# Predictions
predictions = LogisticRegressionModel.predict(X)
print(f"True labels: {[int(i) for i in y]}")
print(f"\nPredictions: {predictions}")
True labels: [0, 0, 0, 1, 1, 1]
Predictions: [0, 0, 0, 1, 1, 1]Suppose you are a health data scientist at a hospital, and you would like to predict a patient’s blood pressure based on their age. Moreover, you would like to predict whether a patient is at risk of hypertension (high blood pressure).
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, LogisticRegression
# Fake dataset we created: Age (years) vs Blood Pressure (mmHg)
age = np.array([25, 30, 35, 40, 45, 50, 55, 60, 65, 70]).reshape(-1,1)
bp = np.array([110, 115, 118, 122, 128, 135, 140, 150, 160, 170])
# Please use Linear Regression to predict blood pressure based on ageThe final results should look like the plot below.
For classifying whether a patient has hypertension or not based on their age, we define hypertension as having a blood pressure greater than 125 mmHg. Please use Logistic Regression to predict the probability of hypertension risk.
# Hypertension if blood pressure > 125 mmHg
risk = (bp >= 125).astype(int)
# Please use Logistic Regression to predict the hypertension risk based on ageThe final results should look similar to the plot below.
