import numpy as np
import matplotlib.pyplot as plt
# Prepare the dataset
data = np.genfromtxt('perceptron_toydata.txt', delimiter='\t')
X, y = data[:, :2], data[:, 2]
y = y.astype(np.int32)
# Shuffle and split the dataset
shuffle_idx = np.arange(y.shape[0])
shuffle_rng = np.random.RandomState(123)
shuffle_rng.shuffle(shuffle_idx)
X, y = X[shuffle_idx], y[shuffle_idx]
# Define the Perceptron model
class Perceptron():
def __init__(self, num_features):
self.num_features = num_features
self.learning_rate = 1.0
self.weights = np.zeros((num_features, 1), dtype=np.float32)
self.bias = np.zeros(1, dtype=np.float32)
def forward(self, x):
linear = np.dot(x, self.weights) + self.bias
predictions = np.where(linear > 0., 1, 0)
return predictions
def backward(self, x, y):
predictions = self.forward(x)
errors = y - predictions
return errors
def train(self, x, y, epochs):
for e in range(epochs):
for i in range(y.shape[0]):
errors = self.backward(x[i].reshape(1, self.num_features), y[i]).reshape(-1)
self.weights += self.learning_rate * (errors * x[i]).reshape(self.num_features, 1)
self.bias += self.learning_rate * errors
def evaluate(self, x, y):
predictions = self.forward(x).reshape(-1)
accuracy = np.sum(predictions == y) / y.shape[0]
return accuracy
# Train the Perceptron model and store weights and biases for each step
all_weights = []
all_biases = []
ppn = Perceptron(num_features=2)
acc = 0
for epoch in range(10):
for i in range(X.shape[0]):
all_weights.append(ppn.weights.copy())
all_biases.append(ppn.bias.copy())
ppn.train(X[i].reshape(1, -1), y[i].reshape(-1), epochs=1)
acc = ppn.evaluate(X, y)
if acc == 1.0: break
if acc == 1.0:
all_weights.append(ppn.weights.copy())
all_biases.append(ppn.bias.copy())
breakModule 4
Introduction to Deep Learning
Class Activities
Week 9
Recap
Examples
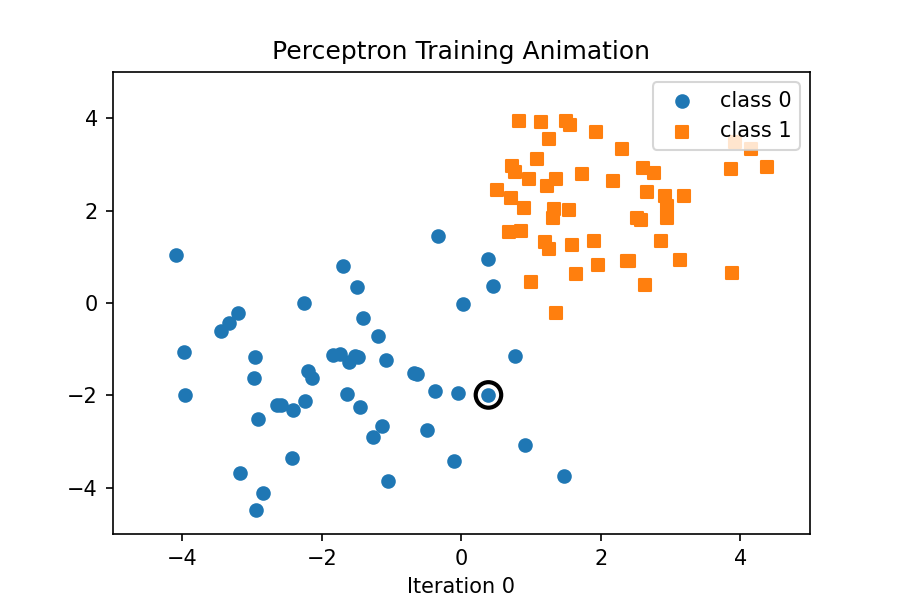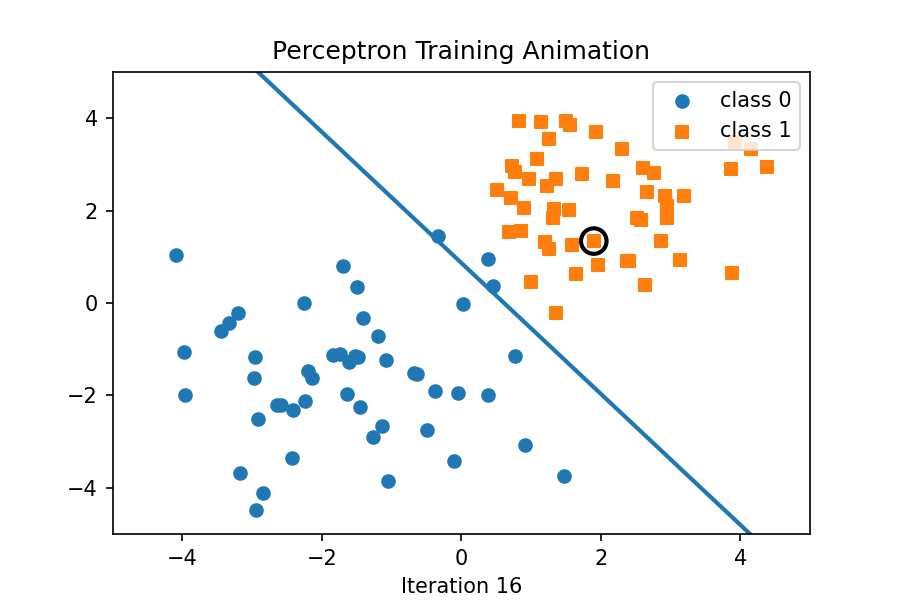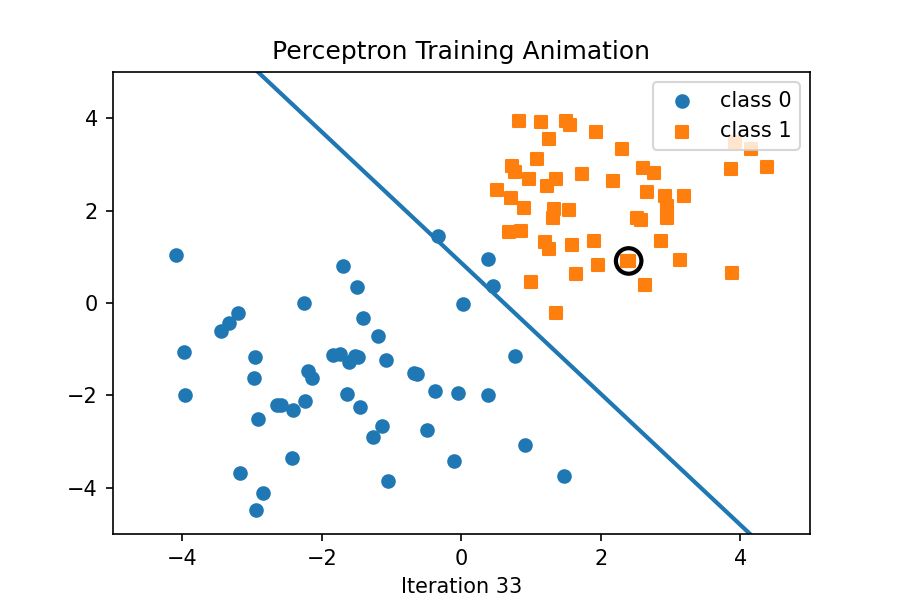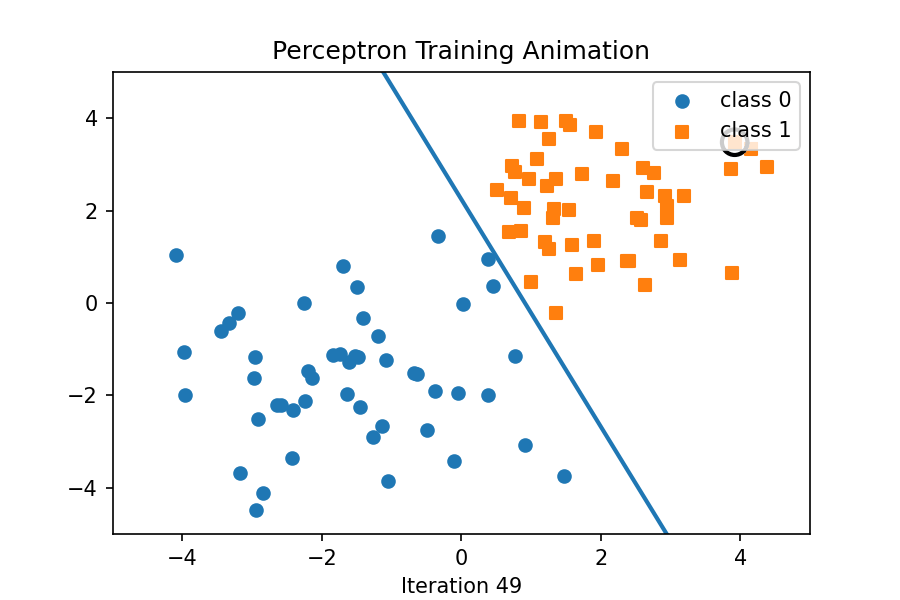
Example 1: Perceptron Animation
In this example, we will implement the Perceptron algorithm from scratch using Python and NumPy. We will visualize the training process by using an animated GIF that shows how the decision boundary evolves as the model learns from the data. That hollow circle is just a visual highlight for the current training sample in that frame. It doesn’t affect the model as it’s there so you can see which point the perceptron just “looked at” or “refers to” when updating the weights and shifting the decision boundary. This following example is modified from here, and the toy dataset can be found here.
Example 2: Implementation of Adaline Linear Neuron in Numpy
In this example, we will implement the Adaline (Adaptive Linear Neuron) algorithm from scratch using Python and NumPy. We will use the classic Iris dataset for training and testing the model. This following example is modified from here.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# Load the Iris dataset
iris = load_iris()
X = iris.data[:, [0, 2]] # Use only two features for simplicity
y = iris.target
y = np.where(y == 0, -1, 1)
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)
# Standardize the features
X_train_std = (X_train - X_train.mean()) / X_train.std()
X_test_std = (X_test - X_train.mean()) / X_train.std()
# Define the Adaline Model
class Adaline:
def __init__(self, learning_rate=0.01, n_iter=50):
self.learning_rate = learning_rate
self.n_iter = n_iter
def fit(self, X, y):
n_samples, n_features = X.shape
self.weights = np.zeros(n_features)
self.bias = 0
self.cost_ = []
for _ in range(self.n_iter):
y_pred = self.activation(X)
error = y - y_pred
self.weights += self.learning_rate * np.dot(X.T, error) # Update weights
self.bias += self.learning_rate * np.sum(error) # Update bias
cost = 0.5 * np.sum(error ** 2)
self.cost_.append(cost)
def activation(self, X):
return np.dot(X, self.weights) + self.bias
def predict(self, X):
return np.where(self.activation(X) >= 0.0, 1, -1)
# Train the Adaline model
adaline_model = Adaline(learning_rate=0.001, n_iter=80)
adaline_model.fit(X_train_std, y_train)
# Plot the cost over epochs
plt.plot(range(1, len(adaline_model.cost_) + 1), adaline_model.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Sum of Squared Errors')
plt.title('Adaline Training Curve')
plt.show()
# Evaluate the Adaline model
y_pred = adaline_model.predict(X_test_std)
accuracy = np.sum(y_test == y_pred) / len(y_test)
print("Accuracy:", accuracy)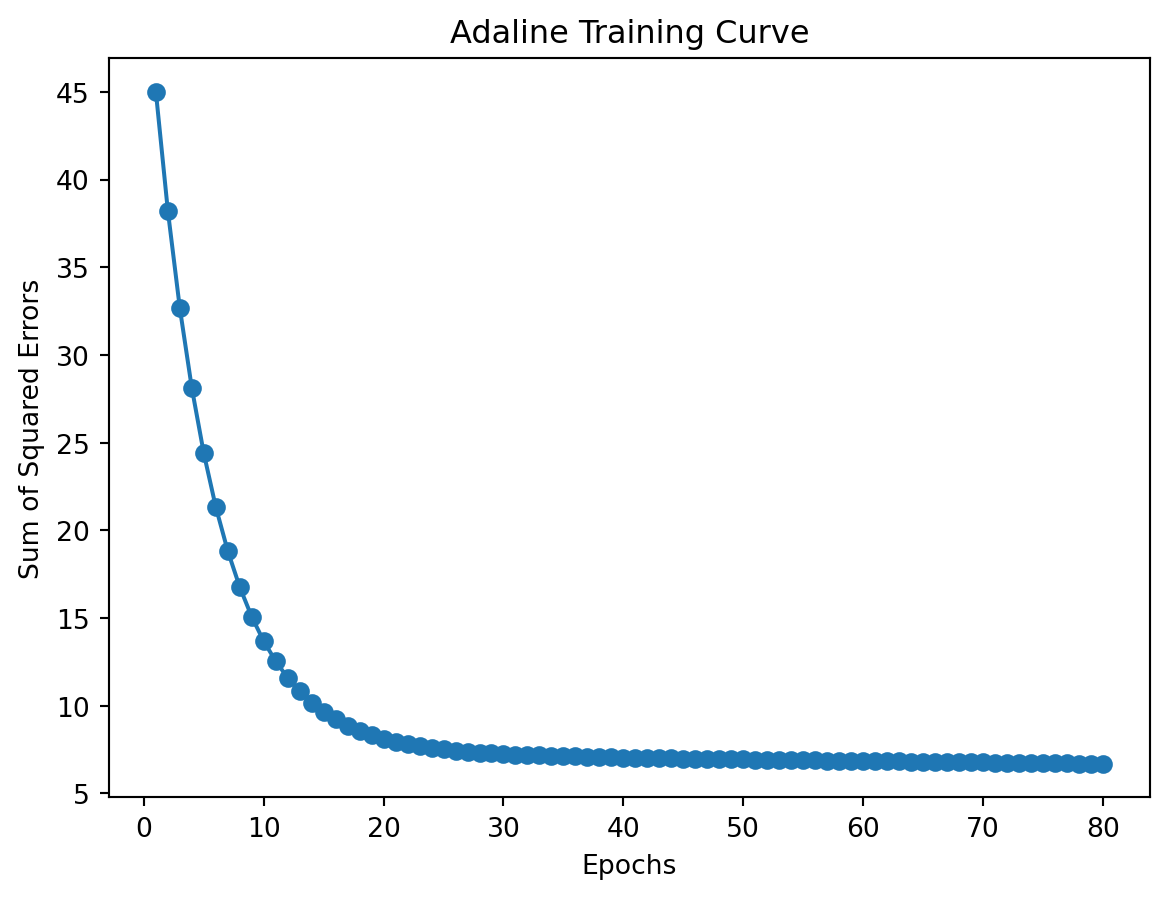
Accuracy: 0.9833333333333333Hands-on Practice
Q1: Please use the Perceptron algorithm from scikit-learn library to train the Iris dataset.
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# Load the Iris dataset
data = load_iris()
# Splitting the dataset to train data and test data
X, y = data.data[:100, :], data.target[:100]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Please write your code below this lineAccuracy: 1.0Q2: Comparing the Adaline and Perceptron model performance on the following synthetic dataset.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
# Generate a synthetic binary classification dataset
X, y = make_classification(
n_samples=4000,
n_features=2,
n_informative=2,
n_redundant=0,
random_state=42,
)
# Plot the generated data points
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y, edgecolor='k', alpha=0.6)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Dataset")
plt.show()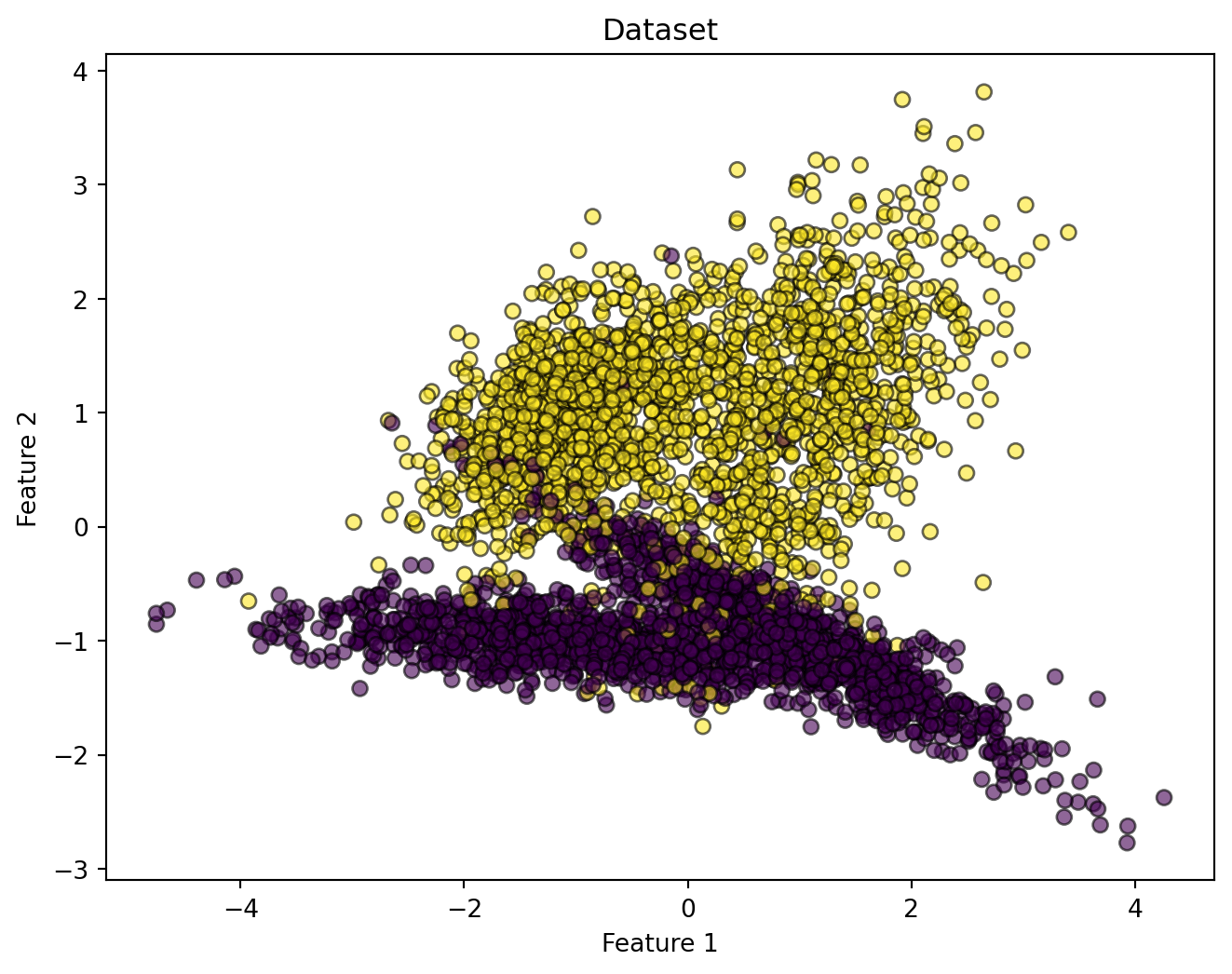
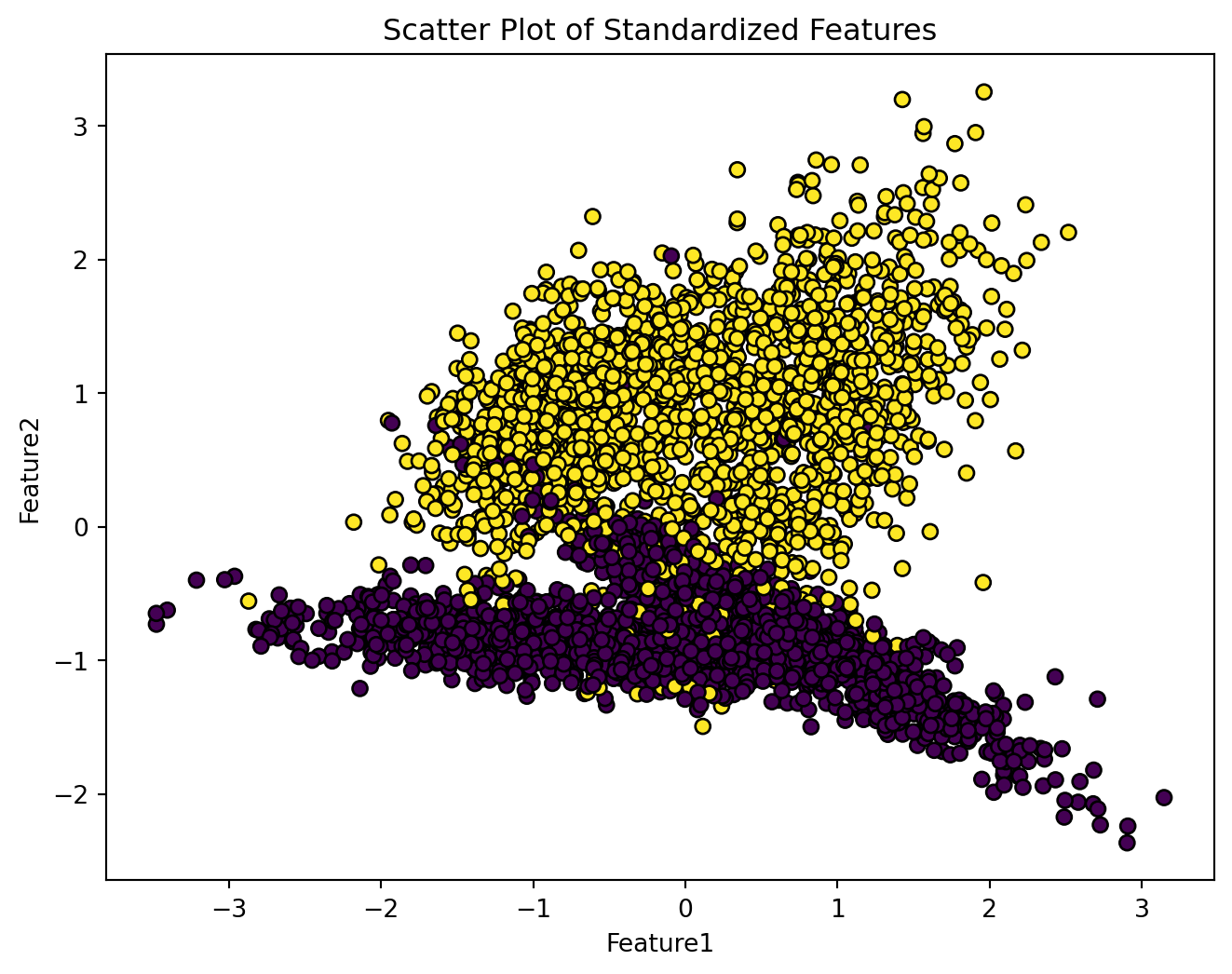
Q2.1: Please standardize the above dataset and store the standardized features in variable X. Afterwards, plot the standardized dataset as showing in the following.
Q2.2: Please split the data into training set and testing set with 80% training data and 20% testing data. Use random state 42 for reproducibility.
# Please write your code below this line
# Split the dataset into training and testing setsTraining set size: 3200 samples
Testing set size: 800 samplesQ2.3: Please implement a Perceptron learning algorithm on the standardized dataset. In this example, we set the learning rate to 0.002 and the number of iterations to 400. You may adjust these two parameters to see how they affect the performance of the model. After training the model, please plot the decision boundary of the Perceptron model.
# Please write your code below this line
# Perceptron model implementation and visualization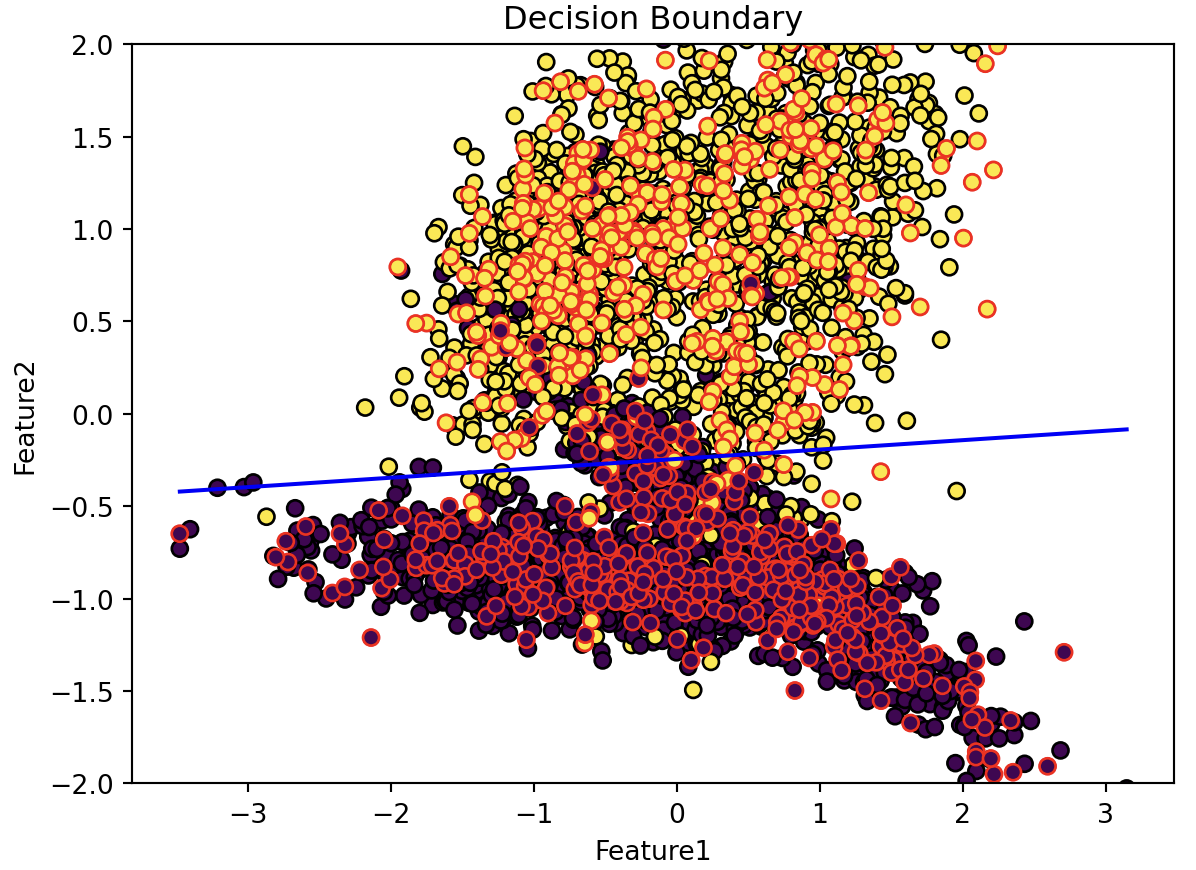
Q2.4: Please implement an Adaline learning algorithm on the standardized dataset. In this example, we set the learning rate to 0.001 and the number of iterations to 400. You may adjust these two parameters to see how they affect the performance of the model. After training the model, please plot the decision boundary of the Adaline model.
# Please write your code below this line
# Adaline model implementation and visualization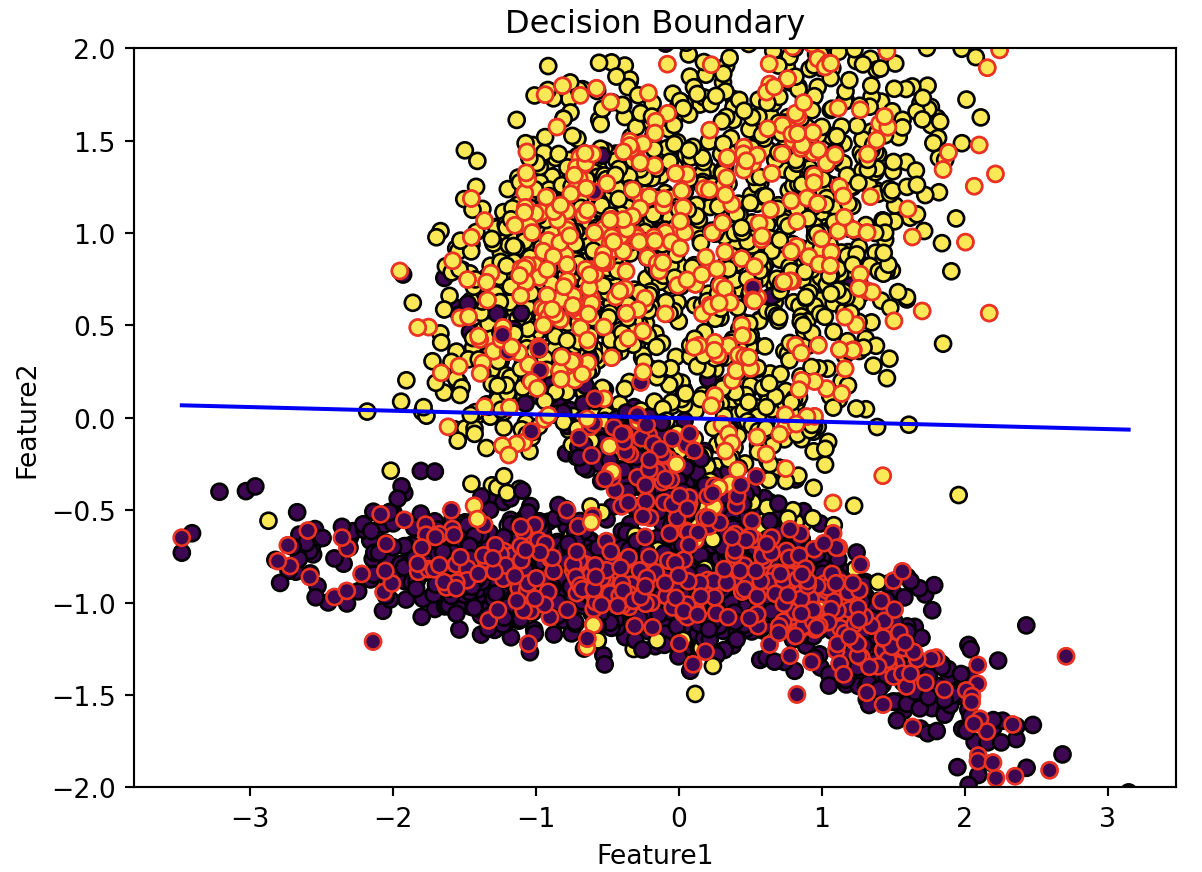
Q2.4: Comparing the accuracy of Adaline and Perceptron using Bar Graph from the matplotlib library.
# Please write your code below this line
# Adaline model implementation and visualization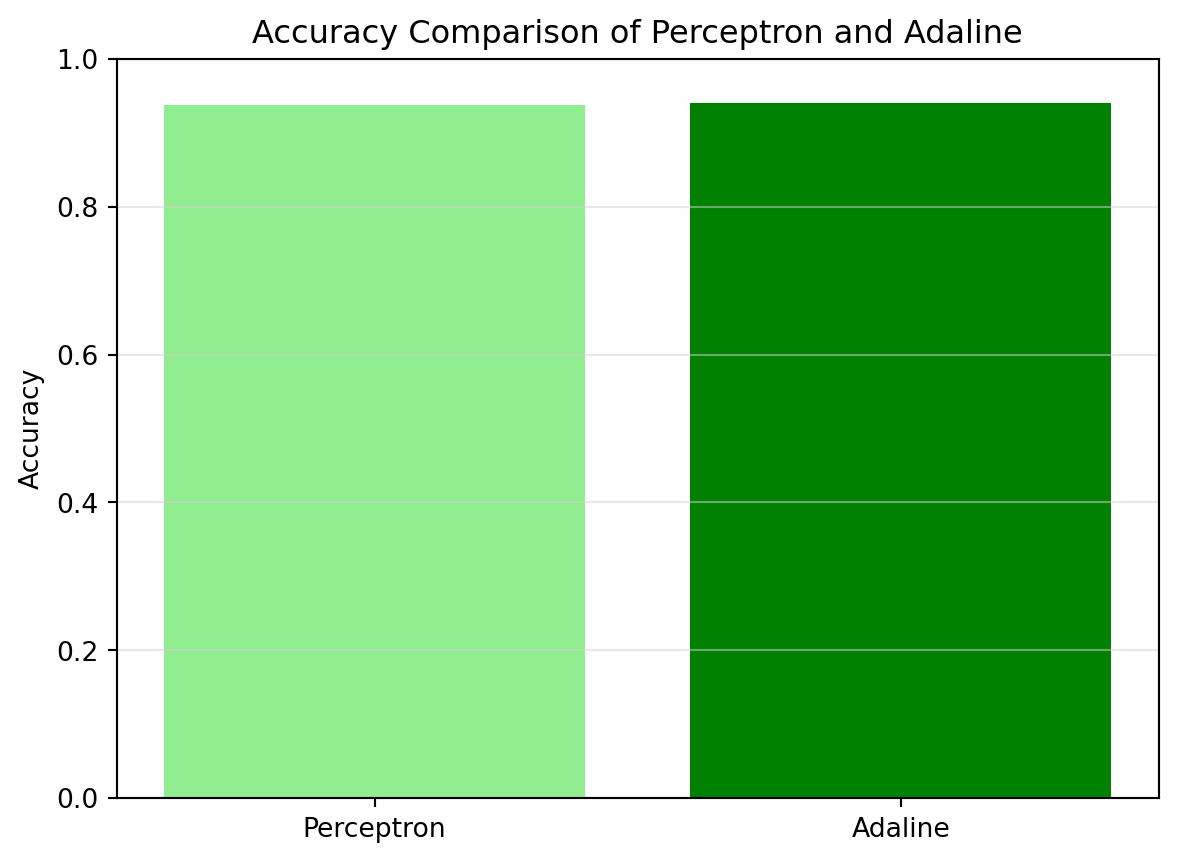
Please note that Q2 is adopted and modified from a kaggle example, and you may find more detailed explaination from the provided link.
Week 10
Recap
Examples
Example 1: Neural Network Forward Propagation
In this example, we will implement a simple feedforward neural network using NumPy and the following code is adopted and modified from here.
import numpy as np
import pandas as pd
data = {'cgpa': [8.5, 9.2, 7.8], 'profile_score': [85, 92, 78], 'lpa': [10, 12, 8]}
df = pd.DataFrame(data)
X = df[['cgpa', 'profile_score']].values
def initialize_parameters():
np.random.seed(1)
W = np.random.randn(2, 1) * 0.01
b = np.zeros((1, 1))
return W, b
def forward_propagation(X, W, b):
# Linear transformation
Z = np.dot(X, W) + b
# Sigmoid activation function
A = 1 / (1 + np.exp(-Z))
return A
W, b = initialize_parameters()
A = forward_propagation(X, W, b)
print("Final Output:\n", A)Final Output:
[[0.40566303]
[0.39810287]
[0.41326819]]Example 2: Neural Network Backward Propagation
In this example, we will implement the backward propagation process for a simple feedforward neural network using NumPy, and the following code is adopted and modified from here.
import numpy as np
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size):
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.weights_input_hidden = np.random.randn(self.input_size, self.hidden_size)
self.weights_hidden_output = np.random.randn(self.hidden_size, self.output_size)
self.bias_hidden = np.zeros((1, self.hidden_size))
self.bias_output = np.zeros((1, self.output_size))
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(self, x):
return x * (1 - x)
def feedforward(self, X):
self.hidden_activation = np.dot(X, self.weights_input_hidden) + self.bias_hidden
self.hidden_output = self.sigmoid(self.hidden_activation)
self.output_activation = np.dot(self.hidden_output, self.weights_hidden_output) + self.bias_output
self.predicted_output = self.sigmoid(self.output_activation)
return self.predicted_output
def backward(self, X, y, learning_rate):
output_error = y - self.predicted_output
output_delta = output_error * self.sigmoid_derivative(self.predicted_output)
hidden_error = np.dot(output_delta, self.weights_hidden_output.T)
hidden_delta = hidden_error * self.sigmoid_derivative(self.hidden_output)
self.weights_hidden_output += np.dot(self.hidden_output.T, output_delta) * learning_rate
self.bias_output += np.sum(output_delta, axis=0, keepdims=True) * learning_rate
self.weights_input_hidden += np.dot(X.T, hidden_delta) * learning_rate
self.bias_hidden += np.sum(hidden_delta, axis=0, keepdims=True) * learning_rate
def train(self, X, y, epochs, learning_rate):
for epoch in range(epochs):
output = self.feedforward(X)
self.backward(X, y, learning_rate)
if epoch % 4000 == 0:
loss = np.mean(np.square(y - output))
print(f"Epoch {epoch}, Loss:{loss}")
# Sample dataset for XOR problem
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
# Target output for the XOR problem
y = np.array([[0], [1], [1], [0]])
# Initialize and Train the Neural Network
nn = NeuralNetwork(input_size=2, hidden_size=4, output_size=1)
nn.train(X, y, epochs=10000, learning_rate=0.1)
output = nn.feedforward(X)
print("Final Predictions after Training:")
print(output)Epoch 0, Loss:0.2587210173837184
Epoch 4000, Loss:0.015890565252111584
Epoch 8000, Loss:0.0033627357847841152
Final Predictions after Training:
[[0.03969706]
[0.96741739]
[0.93734394]
[0.05146935]]Example 3: Building Micrograd
Please refer to this amazing video and code by Andrej Karpathy for building Micrograd.
Hands-on Practice
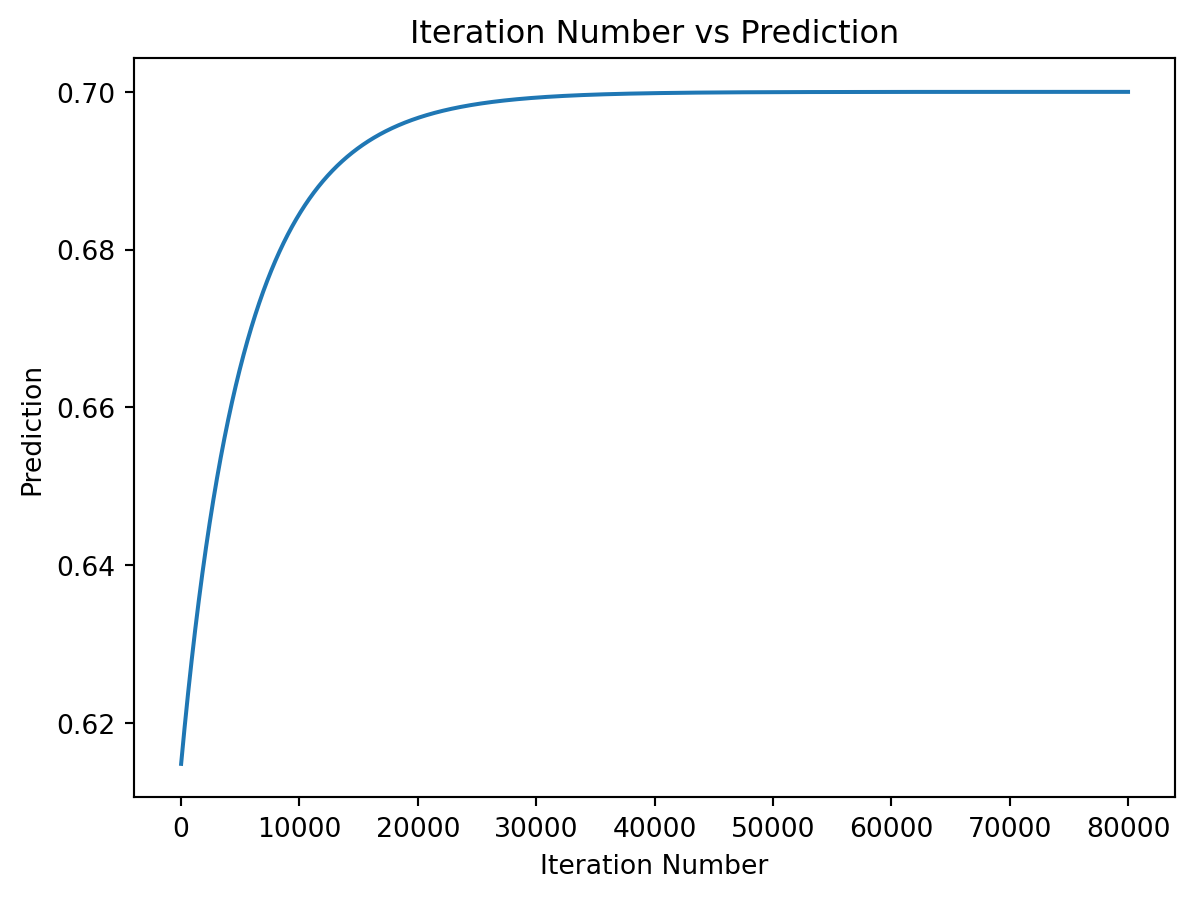
Q1: Coding forward and backward pass in Python. Given the following inputs, weights, and target output, please implement the forward pass to compute the predicted output and the backward pass to update the weights using gradient descent. It is recommended to run for 80000 iterations in this example; however, you may adjust the number of iterations and learning rate to see how they affect the performance of the model. After training the model, please plot the error and predicted output given input x = [0.1, 0.4] over iterations and you should observe that the final prediction result is close to the target value y = 0.7.
import numpy
import matplotlib.pyplot as plt
def sigmoid(sop):
return 1.0/(1+numpy.exp(-1*sop))
def error(predicted, target):
return numpy.power(predicted-target, 2)
def error_predicted_deriv(predicted, target):
return 2*(predicted-target)
def sigmoid_sop_deriv(sop):
return sigmoid(sop)*(1.0-sigmoid(sop))
def sop_w_deriv(x):
return x
def update_w(w, grad, learning_rate):
return w - learning_rate*grad
x1=0.1
x2=0.4
target = 0.7
learning_rate = 0.01
w1=numpy.random.rand()
w2=numpy.random.rand()
predicted_output = []
network_error = []
# Please write your code below this line
# Include forward pass and backward pass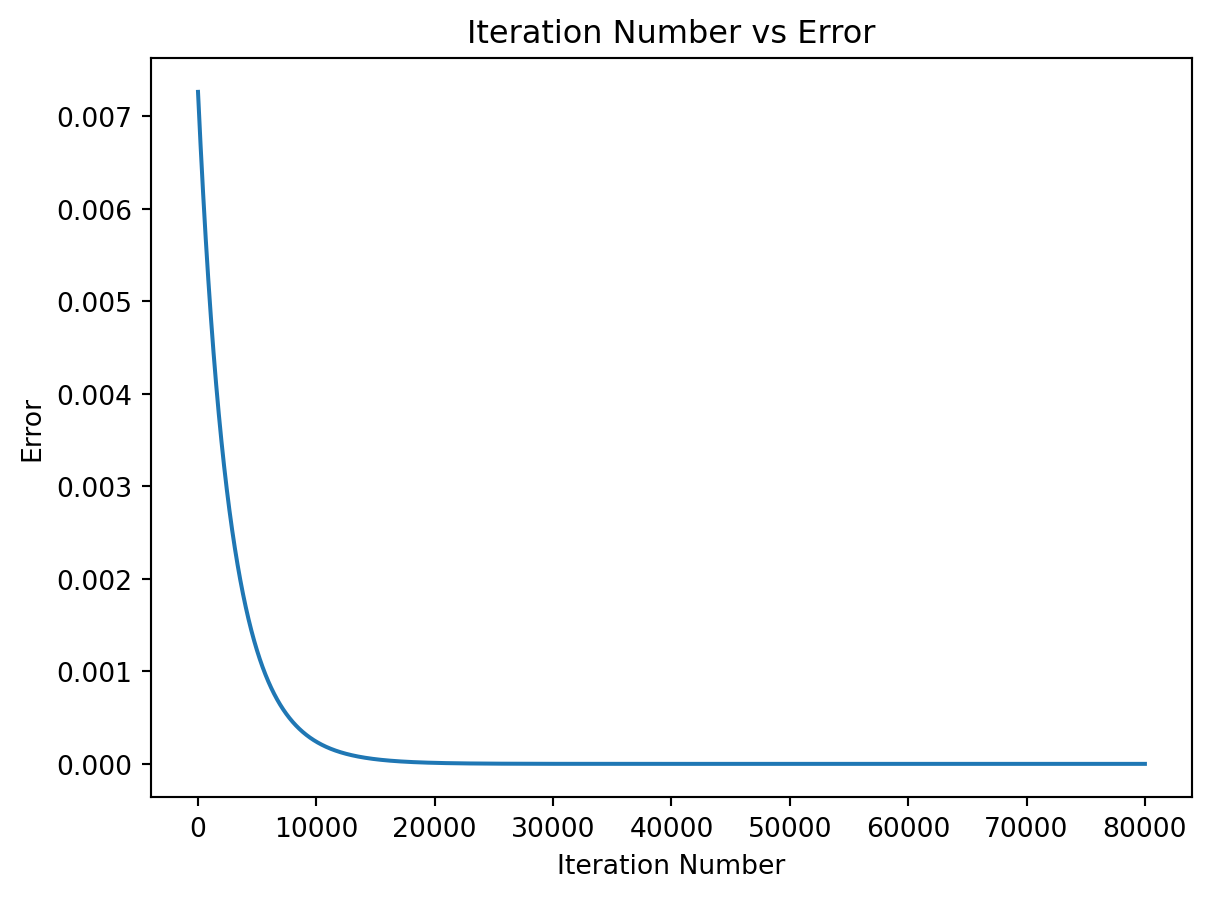
Q2: The following is an example that builds a network with 3 inputs and 1 output. Please use the scikit-learn library to implement the MLPRegressor network. The MLPRegressor model configurations are given below. After training the model, please predict the output given the original input x = [0.1, 0.4, 4.1]. The final prediction result should be close to the target value y = 0.2.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
# Prepare the dataset
x = np.array([0.1, 0.4, 4.1]).reshape(1, -1) # shape (1, 3)
y = np.array([0.2]).ravel() # shape (1,)
# Define the Scikit-learn MLPRegressor model
mlp = MLPRegressor(
hidden_layer_sizes=(7, 5, 4),
activation="logistic",
solver="sgd",
learning_rate="constant",
learning_rate_init=0.05,
momentum=0.9,
max_iter=1,
warm_start=True,
random_state=42,
)
# Parameters setting for the MLPRegressor
mlp = MLPRegressor(
hidden_layer_sizes=(7,5,4),
activation="logistic",
solver="sgd",
learning_rate="constant",
learning_rate_init=0.05,
momentum=0.9,
max_iter=500,
tol=1e-6,
n_iter_no_change=20,
random_state=42,
)
# Please write your code below this line
# Predict the output given the input xFinal Prediction: [0.20030034]
Target Value: [0.2]Please note that Q1 and Q2 are adopted and modified from this website, and you may find more detailed explaination from the provided link.
Week 11
Recap
Installation
Recommended Software Installation
Install useful software for machine learning project management using the following links:
Recommended Python Libraries Installation
Open your terminal (Mac/Linux) or Anaconda Prompt (Windows) and run the following commands:
pip install numpy
pip install pandas
pip install matplotlib
pip install scikit-learn Install popular deep learning libraries to your local machine:
- TensorFlow Installation Guide
- PyTorch Installation Guide
- OpenCV Installation Guide
- Keras Installation Guide
- JAX Installation Guide
Websites for downloading machine learning models and datasets:
Week 12
Examples
Example 1: Introduction to Autoencoders
Please refer to this notebook published by Tensorflow to practice and understand autoencoders.
Example 2: Convolutional Neural Networks (CNNs)
Please refer to this notebook published by Tensorflow to practice and understand CNNs.
Example 3: Convolutional Variational Autoencoder (CVAE)
Please refer to this notebook published by Tensorflow to practice and understand CVAEs.
Hands-on Practice
Q1: Please go through this tutorial link from kaggle to train a convolutional neural networks using the handwritten digits dataset.
Q2: Please go through this beginner guide link from kaggle to train a convolutional neural network using the MNIST dataset.