Module 3

Dimensionality Reduction and Clustering

Class Activities

Week 5

Recap

Link to Google Form

Hands-on Practice

Release Soon

Week 6

Recap

Link to Google Form

Hands-on Practice

Release Soon

Example: Interactive K-Means Clustering Plot

Below is an interactive k-means clustering visualization with animated iterations and a Voronoi overlay. You can adjust the number of clusters using the slider. The data points are randomly initialized from a CSV file hosted on GitHub. The visualization updates the clusters and centroids over 10 iterations.

You pick the number of clusters k, then the plot:

• randomly seeds k centroids,
• repeatedly assigns each point to the nearest centroid,
• updates each centroid to the mean of its assigned points,
• animates those changes over ~10 iterations,
• shows a Voronoi partition (the colored regions), the data points, and the centroid markers.

import {slider, select} from "@jashkenas/inputs"

d3 = require("d3@5")

height = 460.8
margin = {
  return {top: 30, right: 20, bottom: 20, left: 40}
}
xScale = d3.scaleLinear()
      .domain([0,d3.max(data.map(d=>d.x))])
      .range([margin.left, width - margin.right])

yScale = d3.scaleLinear()
      .domain([0,d3.max(data.map(d=>d.y))])
      .range([height - margin.bottom, margin.top])

data = d3.csv("https://raw.githubusercontent.com/will-pang/maching_learning_from_scratch/main/K_Means/data.csv",
                   ({x, y}) => ({x: +x, y: +y}))
viewof k= Inputs.range([1, data.length], {value: 3, step: 1, label: "Clusters"})
html`<div style="margin-bottom: 20px;"></div>`

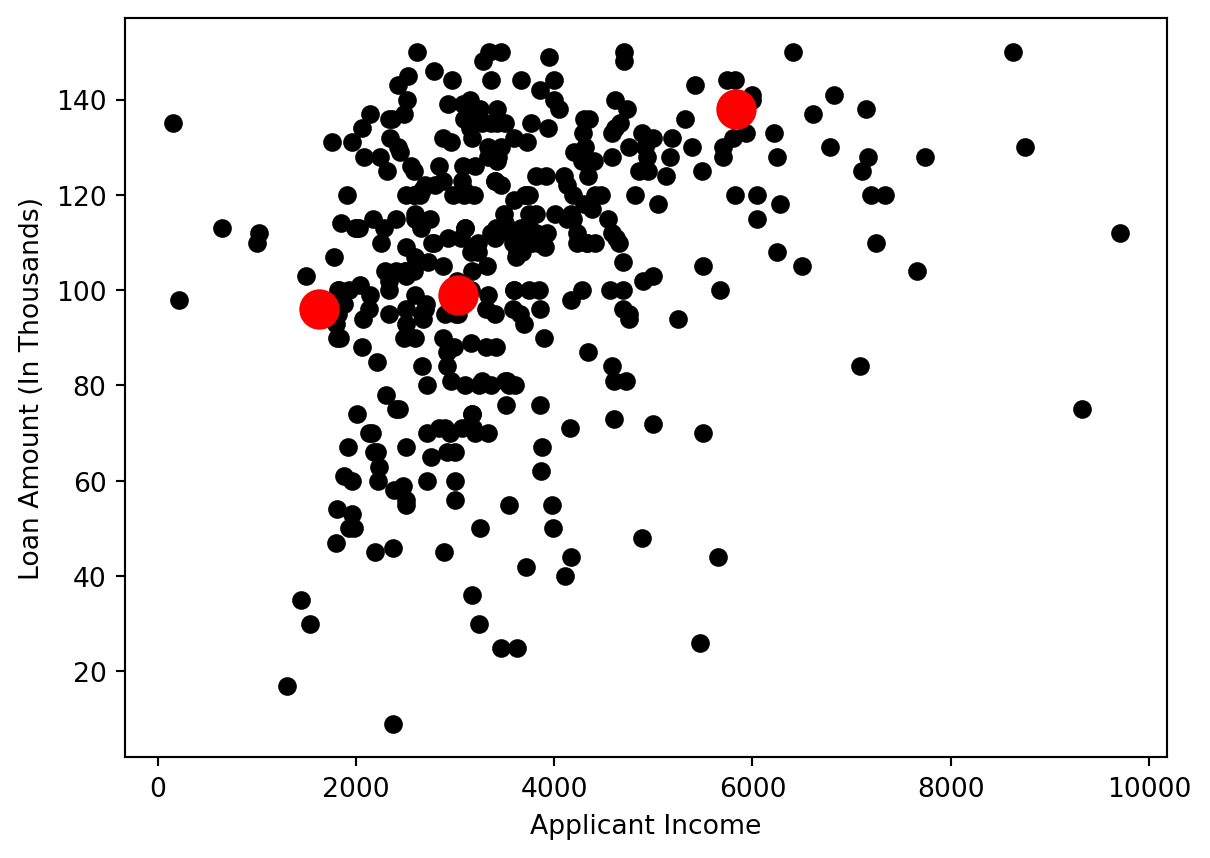
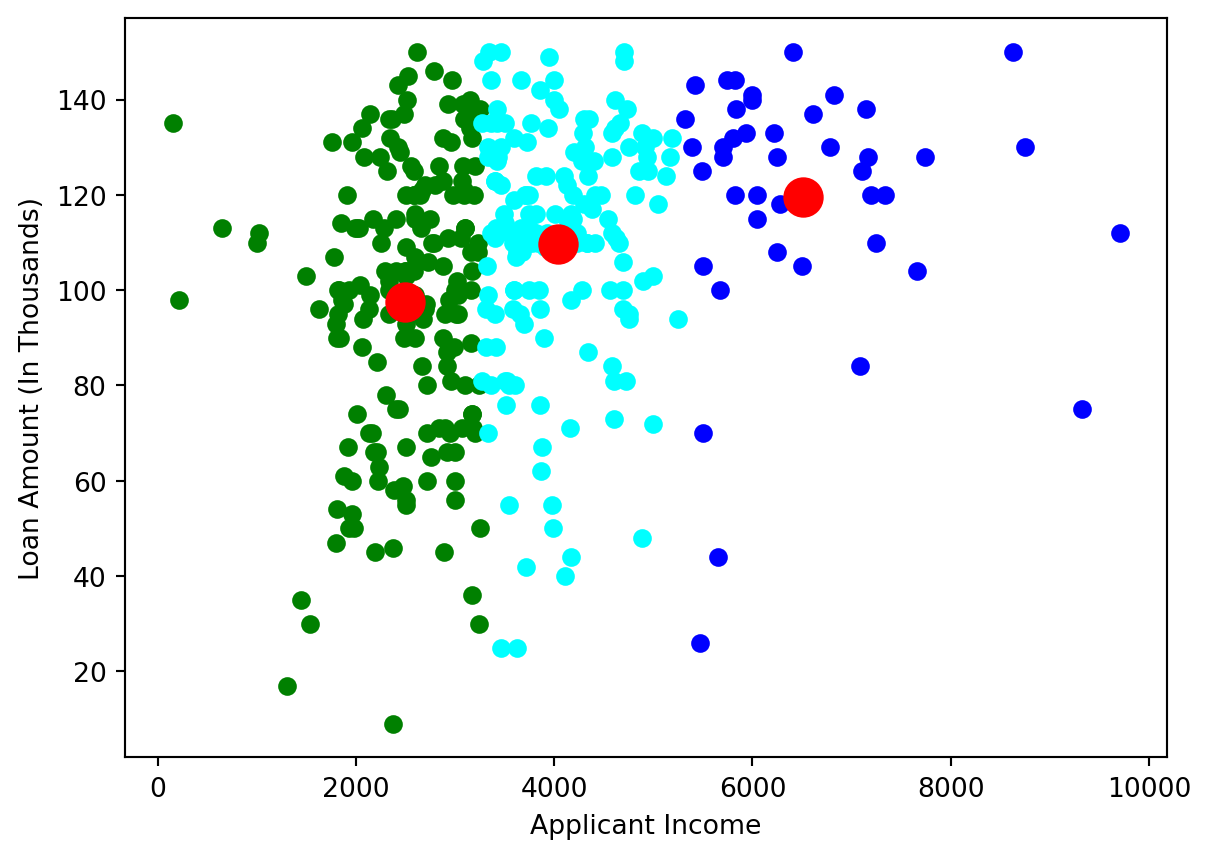
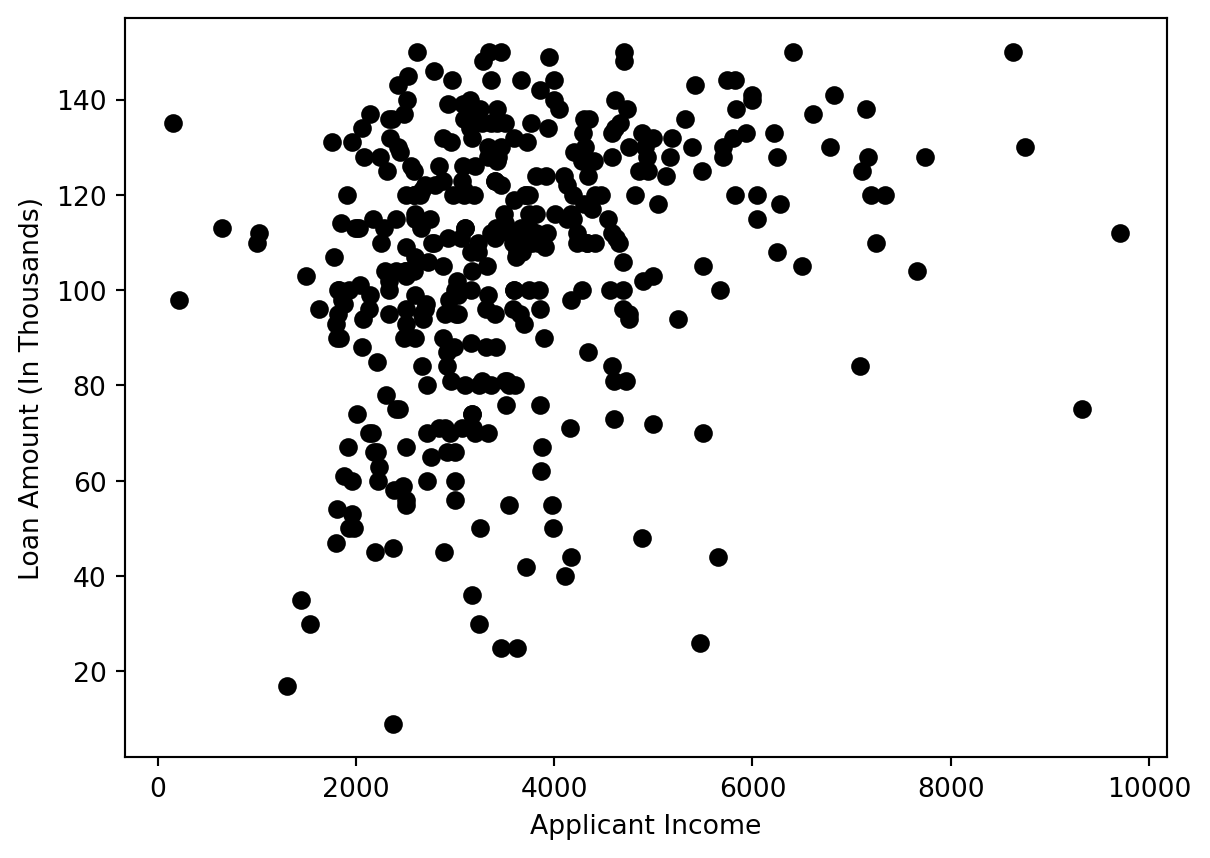
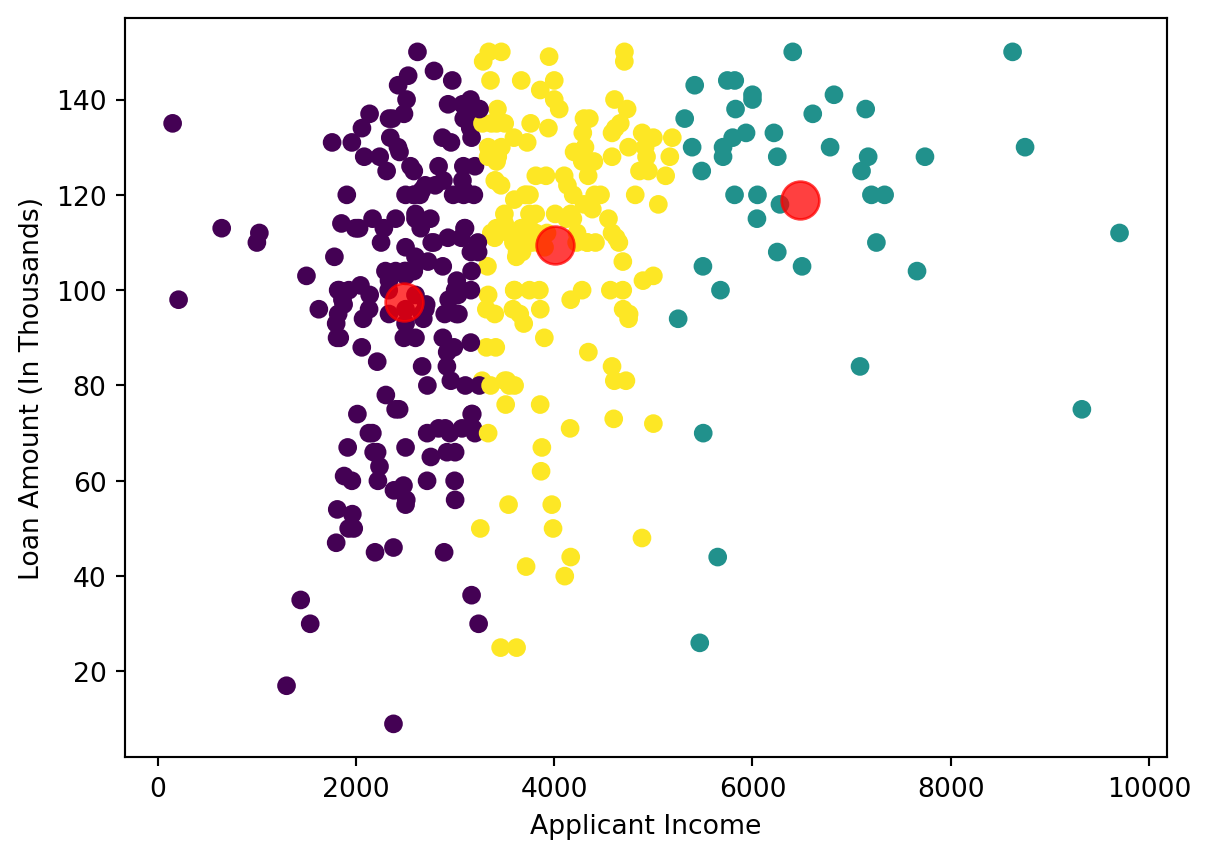
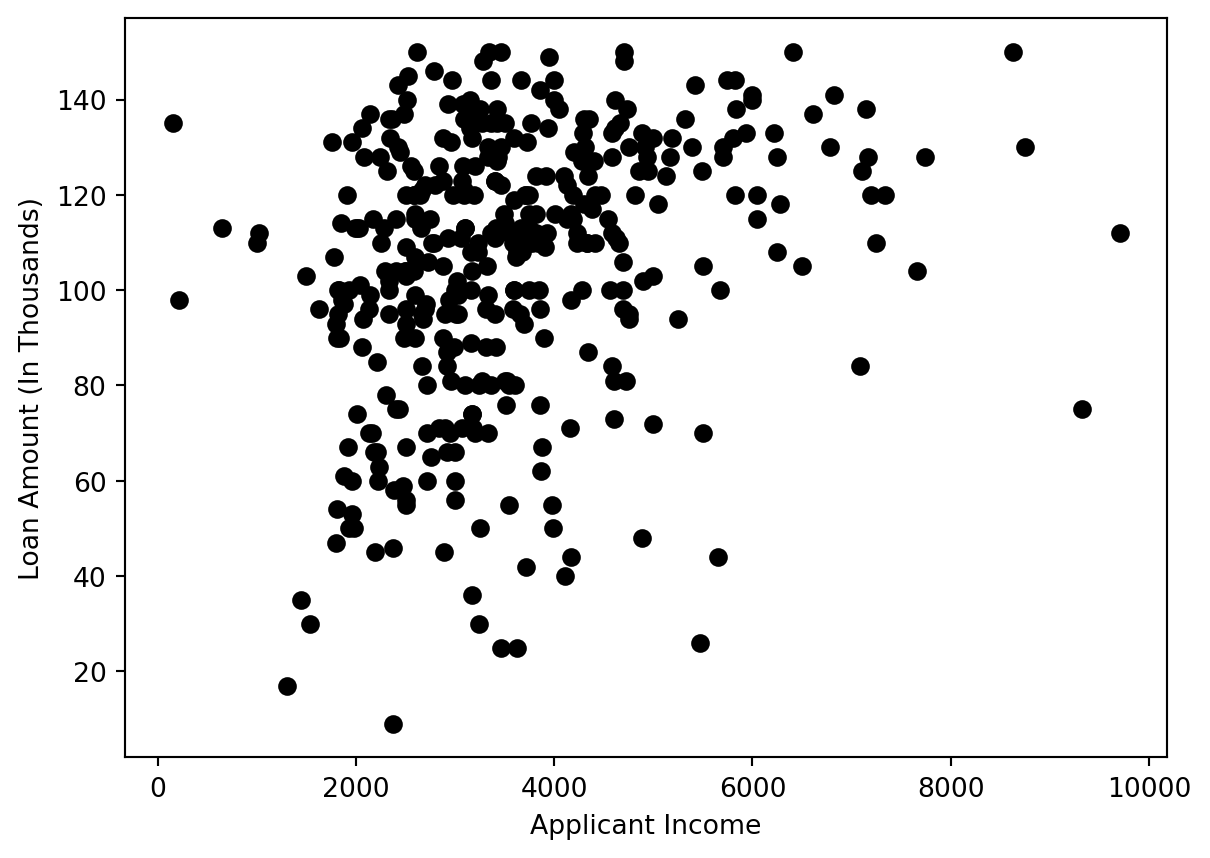
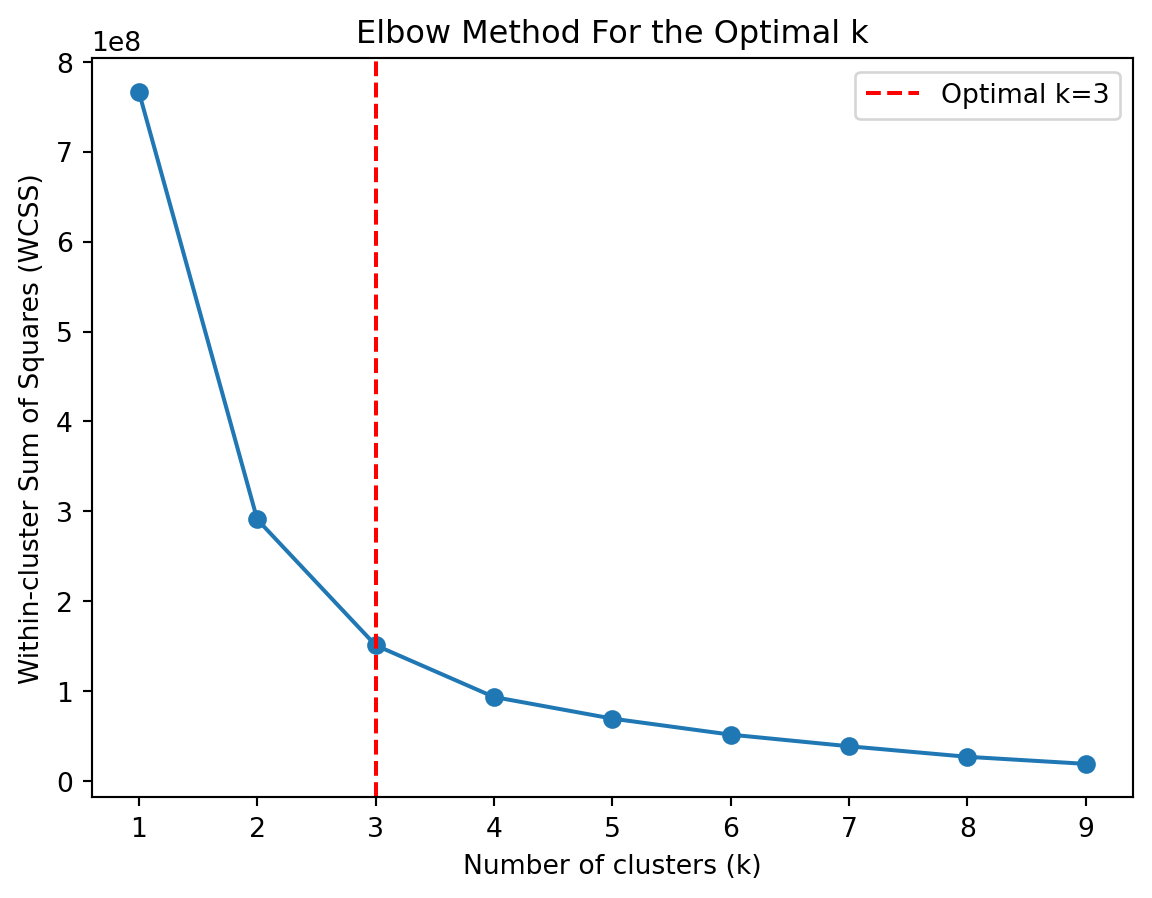
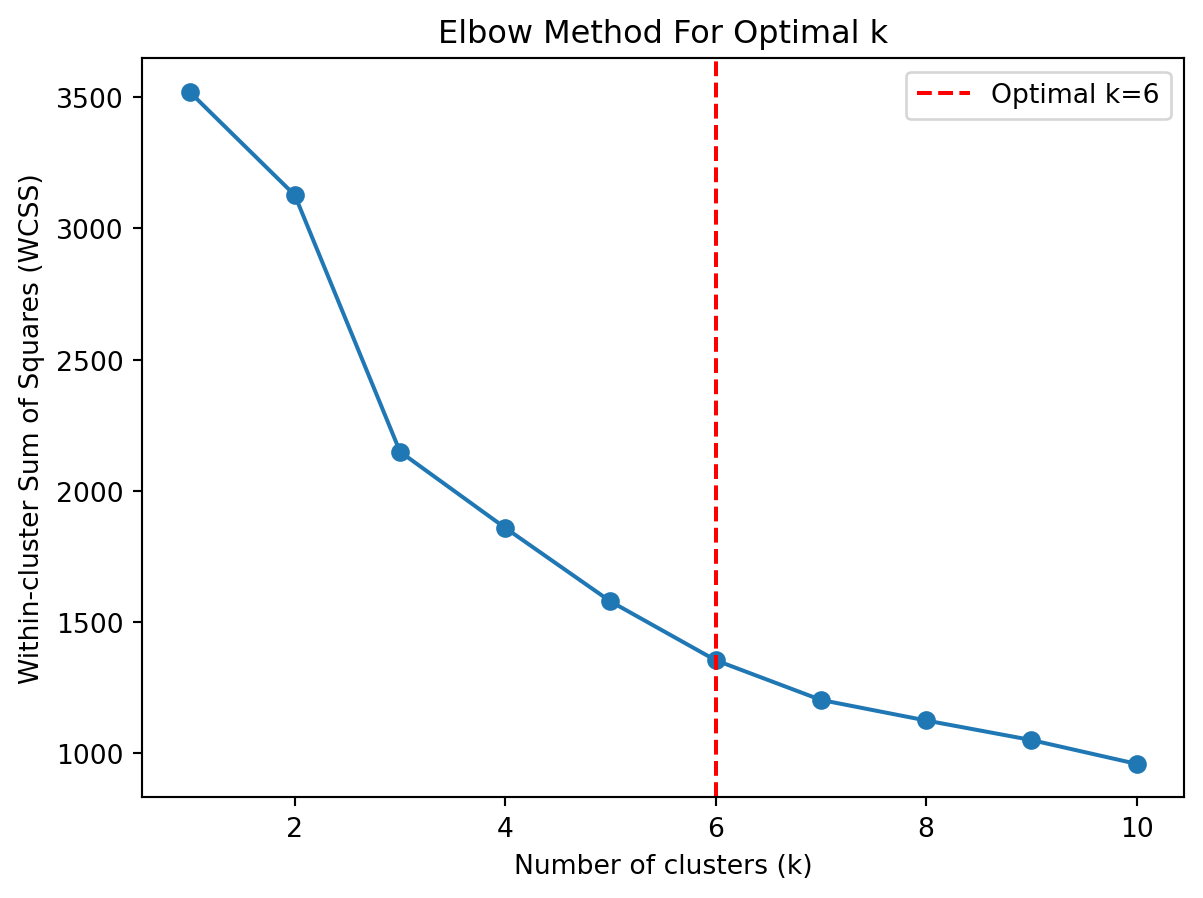
function darken(color, k) {
  return d3.color(color).darker(k).toString();
}

function update(root) {
  const t = d3.transition();

  root.selectAll('.clusters path').data(voronoi.polygons(centroids))
    .transition(t)
    .attr('d', d => d == null ? null : 'M' + d.join('L') + 'Z');

  root.selectAll('.dots circle')
    .transition(t)
    .attr('fill', d => color_scheme_1(d.cluster))
    .attr('cx', d => xScale(d.x))
    .attr('cy', d => yScale(d.y));
  
  root.selectAll('.centers circle')
    .transition(t)
    .attr('cx', d => xScale(d.x))
    .attr('cy', d => yScale(d.y));  
}

centroids = {
  restart;

  return d3.range(k).map(() => {
    return {
      x: data.map(item => item.x)[getRandomInt(data.length)],
      y: data.map(item => item.y)[getRandomInt(data.length)]
  }
})
}

voronoi = d3.voronoi()
  .x(d => xScale(d.x))
  .y(d => yScale(d.y))
  .extent([[0, 0], [width, height]])

color_labels = ["red", "green", "blue", "yellow", "brown", "orange"]

color_scheme_1 = d3.scaleOrdinal()
          .domain(d3.range(k))
          .range(color_labels.map(d => darken(d, 0)))

color_scheme_2 = d3.scaleOrdinal()
          .domain(d3.range(k))
          .range(color_labels.map(d => darken(d, 1)))

function distance(a,b){
  return Math.sqrt((a.x - b.x)**2 + (a.y - b.y)**2)
}

function getRandomInt(max_value){
  return Math.floor(Math.random(1) * max_value);
}

svg = {
  const root = d3.select(DOM.svg(width, height))
    .style("max-width", "100%")
    .style("height", "auto");

  // Clusters
  root.append('g').attr('class', 'clusters').selectAll('path')
    .data(voronoi.polygons(centroids))
    .enter()
    .append('path')
    .attr('d', d => d == null ? null : 'M' + d.join('L') + 'Z')
    //.attr('fill', 'none')
    .attr('fill', (d, i) => color_scheme_1(i))
    .attr('fill-opacity', 0.3)
    .attr('stroke-width', 0.5)
    .attr('stroke', '#000');

  // Dots
  root.append('g').attr('class', 'dots').selectAll('circle').data(data)
    .enter()
    .append('circle')
    .attr('stroke', '#000')
    .attr('stroke-width', 0)
    .attr('fill-opacity', 1.0)
    .attr('r', 3)
    .attr('fill', d => color_scheme_2(d.cluster))
    .attr('cx', d => xScale(d.x))
    .attr('cy', d => yScale(d.y));

  // Centers
  root.append('g').attr('class', 'centers').selectAll('circle').data(centroids)
    .enter()
    .append('circle')
    .attr('r', 5)
    .attr('fill', '#000')
    .attr('fill-opacity', 0.7)
    .attr('cx', d => xScale(d.x))
    .attr('cy', d => yScale(d.y));

  // Update
  update(root);

  return root;
}

svg.node()

{
  for (let i = 0; i < 10; i++) {
    // Assign datapoints into centroids
    data.forEach(d=> {
      // Compute minimum distance between point and cluster(s) and then assign point to cluster with smallest distance
      d.cluster = d3.scan(centroids, (a,b) => distance(a,d) - distance(b,d));
    });

    // Group points into centroid (note, in previous step, we only assigned point to cluster) and calculate new centroids from each cluster
    d3.nest()
      .key(d => d.cluster)
      .sortKeys(d3.ascending)
      .entries(data)
      .forEach(n => {
        // Get average of each centroid by summing over all x's and all y's and dividing it by the length
        let cx = n.values.map(v => v.x).reduce((a,b) => a+b)/n.values.length
        let cy = n.values.map(v => v.y).reduce((a,b) => a+b)/n.values.length
        // Update centroids
        centroids[+n.key].x = cx;
        centroids[+n.key].y = cy;
      });
    // Update SVG
    update(svg);

    yield md`Iteration: ${await Promises.delay(1000, i + 1)} / 10`;
  }
}

viewof restart = html`<button>Restart`